Как найти активную мощность цепи?

Мощность переменного тока

Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: переменный ток, вынужденные электромагнитные колебания

Переменный ток несёт энергию. Поэтому крайне важным является вопрос о мощности в цепи переменного тока.

Пусть и — мгновенные значение напряжения и силы тока на данном участке цепи. Возьмём малый интервал времени — настолько малый, что напряжение и ток не успеют за это время сколько-нибудь измениться; иными словами, величины и можно считать постоянными в течение интервала .

Пусть за время через наш участок прошёл заряд (в соответствии с правилом выбора знака для силы тока заряд считается положительным, если он переносится в положительном направлении, и отрицательным в противном случае). Электрическое поле движущихся зарядов совершило при этом работу

(1)

Точно такую же формулу мы получили в своё время для постоянного тока. Но в данном случае мощность зависит от времени, совершая колебания вместе током и напряжением; поэтому величина (1) называется ещё мгновенной мощностью.

Из-за наличия сдвига фаз сила тока и напряжение на участке не обязаны совпадать по знаку (например, может случиться так, что напряжение положительно, а сила тока отрицательна, или наоборот). Соответственно, мощность может быть как положительной, так и отрицательной. Рассмотрим чуть подробнее оба этих случая.

1. Мощность положительна: . Напряжение и сила тока имеют одинаковые знаки. Это означает, что направление тока совпадает с направлением электрического поля зарядов, образующих ток. В таком случае энергия участка возрастает: она поступает на данный участок из внешней цепи (например, конденсатор заряжается).

2. Мощность отрицательна: . Напряжение и сила тока имеют разные знаки. Стало быть, ток течёт против поля движущихся зарядов, образующих этот самый ток.

Как такое может случиться? Очень просто: электрическое поле, возникающее на участке, как бы «перевешивает» поле движущихся зарядов и «продавливает» ток против этого поля. В таком случае энергия участка убывает: участок отдаёт энергию во внешнюю цепь (например, конденсатор разряжается).

Если вы не вполне поняли, о чём только что шла речь, не переживайте — дальше будут конкретные примеры, на которых вы всё и увидите.

Мощность тока через резистор

Пусть переменный ток протекает через резистор сопротивлением . Напряжение на резисторе, как нам известно, колеблется в фазе с током:

Поэтому для мгновенной мощности получаем:

(2)

График зависимости мощности (2) от времени представлен на рис. 1. Мы видим, что мощность всё время неотрицательна — резистор забирает энергию из цепи, но не возвращает её обратно в цепь.

Рис. 1. Мощность переменного тока через резистор

Максимальное значение нашей мощности связано с амплитудами тока и напряжения привычными формулами:

Посмотрите ещё раз внимательно на рис. 1. Не возникает ли у вас интуитивное ощущение, что средняя мощность соответствует «середине» нашей синусоиды и принимает поэтому значение ?

Это ощущение совершенно верное! Так оно и есть. Разумеется, можно дать математически строгое определение среднего значения функции (в виде некоторого интеграла) и подтвердить нашу догадку прямым вычислением, но нам это не нужно. Достаточно интуитивного понимания простого и важного факта:

среднее значение квадрата синуса (или косинуса) за период равно .

Этот факт иллюстрируется рисунком 2.

Рис. 2. Среднее значение квадрата синуса равно

Итак, для среднего значения мощности тока на резисторе имеем:

(3)

В связи с этими формулами вводятся так называемые действующие (или эффективные) значения напряжения и силы тока (на самом деле это есть не что иное, как средние квадратические значения напряжения и тока. Такое у нас уже встречалось: средняя квадратическая скорость молекул идеального газа (листок «Уравнение состояния идеального газа»):

(4)

Поэтому если вы возьмёте лампочку, подключите её сначала к источнику постоянного напряжения , а затем к источнику переменного напряжения с таким же действующим значением , то в обоих случаях лампочка будет гореть одинаково ярко.

Действующие значения (4) чрезвычайно важны для практики. Оказывается, вольтметры и амперметры переменного тока показывают именно действующие значения (так уж они устроены). Знайте также, что пресловутые вольт из розетки — это действующее значение напряжения бытовой электросети.

Мощность тока через конденсатор

Пусть на конденсатор подано переменное напряжение . Как мы знаем, ток через конденсатор опережает по фазе напряжение на :

Для мгновенной мощности получаем:

График зависимости мгновенной мощности от времени представлен на рис. 3.

Рис. 3. Мощность переменного тока через конденсатор

Чему равно среднее значение мощности? Оно соответствует «середине» синусоиды и в данном случае равно нулю! Мы видим это сейчас как математический факт. Но интересно было бы с физической точки зрения понять, почему мощность тока через конденсатор оказывается нулевой.

Для этого давайте нарисуем графики напряжения и силы тока в конденсаторе на протяжении одного периода колебаний (рис. 4).

Рис. 4. Напряжение на конденсаторе и сила тока через него

Рассмотрим последовательно все четыре четверти периода.

Мгновенная мощность положительна: конденсатор накапливает энергию, поступающую из внешней цепи. Эта энергия возникает за счёт работы внешнего электрического поля, продвигающего заряды на конденсатор.

2. Вторая четверть, . Напряжение продолжает оставаться положительным, но идёт на убыль. Ток меняет направление и становится отрицательным: конденсатор разряжается против направления внешнего электрического поля.В конце второй четверти конденсатор полностью разряжен.

Мгновенная мощность отрицательна: конденсатор отдаёт энергию. Эта энергия возвращается в цепь: она идёт на совершение работы против электрического поля внешней цепи (конденсатор как бы «продавливает» заряды в направлении, противоположном тому, в котором внешнее поле «хочет» их двигать).

3. Третья четверть, . Внешнее электрическое поле меняет направление: напряжение отрицательно и возрастает по модулю. Сила тока отрицательна: идёт зарядка конденсатора в отрицательном направлении.

Ситуация полностью аналогична первой четверти, только знаки напряжения и тока — противоположные. Мощность положительна: конденсатор вновь накапливает энергию.

4. Четвёртая четверть, . Напряжение отрицательно и убывает по модулю. Конденсатор разряжается против внешнего поля: сила тока положительна.

Мы видим, что энергия, забранная конденсатором из внешней цепи в ходе первой четверти периода колебаний, полностью возвращается в цепь в ходе второй четверти. Затем этот процесс повторяется вновь и вновь. Вот почему средняя мощность, потребляемая конденсатором, оказывается нулевой.

Мощность тока через катушку

Пусть на катушку подано переменное напряжение . Ток через катушку отстаёт по фазе от напряжения на :

Для мгновенной мощности получаем:

Снова средняя мощность оказывается равной нулю. Причины этого, в общем-то, те же, что и в случае с конденсатором. Рассмотрим графики напряжения и силы тока через катушку за период (рис. 5).

Рис. 5. Напряжение на катушке и сила тока через неё

Мы видим, что в течение второй и четвёртой четвертей периода энергия поступает в катушку из внешней цепи. В самом деле, напряжение и сила тока имеют одинаковые знаки, сила тока возрастает по модулю; для создания тока внешнее электрическое поле совершает работу против вихревого электрического поля, и эта работа идёт на увеличение энергии магнитного поля катушки.

В первой и третьей четвертях периода напряжение и сила тока имеют разные знаки: катушка возвращает энергию в цепь. Вихревое электрическое поле, поддерживающее убывающий ток, двигает заряды против внешнего электрического поля и совершает тем самым положительную работу. А за счёт чего совершается эта работа? За счёт энергии, накопленной ранее в катушке.

Таким образом, энергия, запасаемая в катушке за одну четверть периода, полностью возвращается в цепь в ходе следующей четверти. Поэтому средняя мощность, потребляемая катушкой, оказывается равной нулю.

Мощность тока на произвольном участке

Теперь рассмотрим самый общий случай. Пусть имеется произвольный участок цепи — он может содержать резисторы, конденсаторы, катушки…На этот участок подано переменное напряжение .

Как мы знаем из предыдущего листка «Переменный ток. 2», между напряжением и силой тока на данном участке имеется некоторый сдвиг фаз . Мы записывали это так:

Тогда для мгновенной мощности имеем:

(5)

Теперь нам хотелось бы определить, чему равна средняя мощность. Для этого мы преобразуем выражение (5), используя формулу:

В результате получим:

(6)

(7)

Данную формулу можно записать с помощью действующих значений (4) напряжения и силы тока:

Формула (7) охватывает все три рассмотренные выше ситуации. В случае резистора имеем , и мы приходим к формуле (3). Для конденсатора и катушки , и средняя мощность равна нулю.

Кроме того, формула (7) даёт представление о весьма общей проблеме, связанной с передачей электроэнергии. Чрезвычайно важно, чтобы у потребителя был как можно ближе к единице. Иначе потребитель начнёт возвращать значительную часть энергии назад в сеть (что ему совсем невыгодно), и к тому же возвращаемая энергия будет безвозвратно расходоваться на нагревание проводов и других элементов цепи.

Источник: https://ege-study.ru/ru/ege/materialy/fizika/moshhnost-peremennogo-toka/

Реактивная и активная мощность: как найти по формуле, в чем измеряется

Многие люди, которые изучают скалярные физические величины и такие сферы точных наук, как электродинамика, электростатика и магнитостатика, сталкиваются с понятием мощности. Каково определение активной и реактивной мощности, их источник и в чем основная разница — далее в статье.

Описание явлений

Мощностью называется скалярный вид физической величина, которая показывает, как передается или преобразуется электроэнергия. Бывает мощность постоянного и переменного тока. Что касается последнего, то делится на активную и реактивную.

Разновидности

Активной называется полезная сила, определяющая процесс прямого преобразования электроэнергии в необходимый вид силы. В каждом электроприборе преобразовывается она по-своему. К примеру, в лампочке получается свет с теплом, в утюге — тепло, а в электрическом двигателе — механическая энергия. Соответственно, показывает КПД устройства.

Реактивной называется та, которая определяется при помощи электромагнитного поля. Образуется при работе электроприборов.

Обратите внимание! Это вредная и паразитная мощностная характеристика, которая определяется тем, каков характер нагрузки. Для лампочки она равняется нулю, а для электродвигателя она может быть равна большим значениям.

Основные понятия из учебного пособия

Зачем нужна

Электричество передает энергию в проводник для осуществления технического процесса. Чтобы процесс происходил, переданная сила должна преобразовываться в тепло и напряжение. При этом электроэнергия должна поступать постоянно, что обеспечивается обеими разновидностями мощностной характеристики. Активно действующая дает полезную силу, а реактивно действующая ее поддерживает в электродвигательных, трансформаторных, печных, сварочных, дроссельных и осветительных установках.

Значение

Источник реактивной энергии

Чтобы понять природу появления этой энергии и то, как найти реактивную мощность, нужно уточнить, что любая электромагнитная или индукционная машина, которая работает на переменном токе, преобразует электричество в тепло. Чтобы это преобразование произошло, нужно магнитное поле. Оно, соответственно, формируется безваттной энергией. Причина в поглощении энергии индукционной цепи и отдаче ее обратно при спаде магнитного поля два раза за цикл мощностной частоты.

Природа явления

Различия

Разница между величинами в том, что активно действующая мощностная характеристика показывает КПД устройств, а реактивная является передачей этого КПД. Разница также наблюдается в определении, символе, формуле и значимости.

Основная разница

Расчет по формуле

Представить обе разновидности можно определением из формул вычисления. Так активно действующая мощностная характеристика это соотношение напряжения с силой тока на косинус угла сдвига фаз между ними. Там, где несинусоидальный ток, она равна суммированию средних мощностных характеристик. Может быть выражена через другую формулу. Она может быть равна удвоенной силе тока на сопротивление цепи или удвоенному напряжению на проводимость. Также может быть найдена с помощью полной энергии, перемноженной на косинус угла сдвига фаз напряжения с электротоком.

Формула через полную мощностную характеристику

Возвращаясь к вопросу, в каких единицах выражается реактивная мощность потребителей, можно отметить, что она находится по двум формулам, основной из которых является умножение напряжения на силу тока и синус сдвига фаз. Также может быть найдена через квадрат вычисления удвоенной полной энергии потребления. Измерение полной происходит из умножения напряжения на токовую силу.

Обратите внимание! Обе разновидности находятся в ваттах. Один ватт равен килограмму, умноженному на соотношение квадратного метра на кубические секунды. Также он равен джоулю, поделенному на секунды, ньютону на метр/секунду, вольту на ампер.

Отыскать одну и другую силу можно не только по формулам, но и по технологически современным устройствам, таким как вольтметр, амперметр или фазометр. Для вычисления любых показателей можно воспользоваться также мультиметром.

Физические формулы нахождения величин

Мощность — то, что характеризует скорость передачи с преобразованием электроэнергии. Реактивная мощность в цепи переменного тока от активной отличается тем, что используется для передачи реальной силы источника, в то время как вторая является самой реальной электроэнергией. Обе измеряются в ваттах и имеют большое значение в электромагнитном излучении, механической форме генератора или акустической волне. Активно применяются в промышленности.

Источник: https://rusenergetics.ru/ustroistvo/reaktivnaya-moschnost

Активная мощность: формула, как определить — Asutpp

Мощностные характеристики установки или сети являются основными для большинства известных электрических приборов. Активная мощность (проходящая, потребляема) характеризует часть полной мощности, которая передается за определенный период частоты переменного тока.

Определение

Активная и реактивная мощность может быть только у переменного тока, т. к. характеристики сети (силы тока и напряжения) у постоянного всегда равны. Единица измерений активной мощности  Ватт, в то время, как реактивной – реактивный вольтампер и килоВАР (кВАР). Стоит отметить, что как полная, так и активная характеристики могут измеряться в кВт и кВА, это зависит от параметров конкретного устройства и сети. В промышленных цепях чаще всего измеряется в килоВаттах.

Соотношение энергий

Электротехника используется активную составляющую в качестве измерения передачи энергии отдельными электрическими приборами. Рассмотрим, сколько мощности потребляют некоторые из них:

Прибор	Мощность бытовых приборов, Вт/час
Зарядное устройство	2
Люминесцентная лампа ДРЛ	От 50
Акустическая система	30
Электрический чайник	1500
Стиральной машины	2500
Полуавтоматический инвертор	3500
Мойка высокого давления	3500

Исходя из всего, сказанного выше, активная мощность – это положительная характеристика конкретной электрической цепи, которая является одним из основных параметров для выбора электрических приборов и контроля расхода электричества.

Генерация активной составляющей

Обозначение реактивной составляющей:

Это  номинальная величина, которая характеризует нагрузки в электрических устройствах при помощи колебаний ЭМП и потери при работе прибора. Иными словами, передаваемая энергия переходит на определенный реактивный преобразователь (это конденсатор, диодный мост и т. д.) и проявляется только в том случае, если система включает в себя эту составляющую.

Расчет

Для выяснения показателя активной мощности, необходимо знать полную мощность, для её вычисления используется следующая формула:

S = U \ I, где U – это напряжение сети, а I – это сила тока сети.

Этот же расчет выполняется при вычислении уровня передачи энергии катушки при симметричном подключении. Схема имеет следующий вид:

Схема симметричной нагрузки

Расчет активной мощности учитывает угол сдвига фаз или коэффициент (cos φ), тогда:

S = U * I * cos φ.

Очень важным фактором является то, что эта электрическая величина может быть как положительной, так и отрицательной. Это зависит от того, какие характеристики имеет cos φ. Если у синусоидального тока угол сдвига фаз находится в пределах от 0 до 90 градусов, то активная мощность положительная, если от 0 до -90 – то отрицательная. Правило действительно только для синхронного (синусоидального) тока (применяемого для работы асинхронного двигателя, станочного оборудования).

Расчет трехфазной сети

Максимальная и активная обозначается P, реактивная мощность – Q.

Из-за того, что реактивная обуславливается движением и энергией магнитного поля, её формула (с учетом угла сдвига фаз) имеет следующий вид:

QL = ULI = I2xL

Для несинусоидального тока очень сложно подобрать стандартные параметры сети. Для определения нужных характеристик с целью вычисления активной и реактивной мощности используются различные измерительные устройства. Это вольтметр, амперметр и прочие. Исходя от уровня нагрузки, подбирается нужная формула.

Из-за того, что реактивная и активная характеристики связаны с полной мощностью, их соотношение (баланс) имеет следующий вид:

S = √P2 + Q2, и все это равняется U*I .

Но если ток проходит непосредственно по реактивному сопротивлению. То потерь в сети не возникает. Это обуславливает индуктивная индуктивная составляющая – С и сопротивление – L. Эти показатели рассчитываются по формулам:

Сопротивление индуктивности: xL = ωL = 2πfL,

Сопротивление емкости: хc = 1/(ωC) = 1/(2πfC).

Для определения соотношения активной и реактивной мощности используется специальный коэффициент. Это очень важный параметр, по которому можно определить, какая часть энергии используется не по назначению или «теряется» при работе устройства.

При наличии в сети активной реактивной составляющей обязательно должен рассчитываться коэффициент мощности. Эта величина не имеет единиц измерения, она характеризует конкретного потребителя тока, если электрическая система содержит реактивные элементы. С помощью этого показателя становится понятным, в каком направлении и как сдвигается энергия относительно напряжения сети. Для этого понадобится диаграмма треугольников напряжений:

Диаграмма треугольников напряжений

К примеру, при наличии конденсатора формула коэффициента имеет следующий вид:

cos φ = r/z = P/S

Для получения максимально точных результатов рекомендуется не округлять полученные данные.

Компенсация

Учитывая, что при резонансе токов реактивная мощность равняется 0:

Q = QL — QC = ULI – UCI

Для того чтобы улучшить качество работы определенного устройства применяются специальные приборы, минимизирующие воздействие потерь на сеть. В частности, это ИБП. В данном приборе не нуждаются электрические потребители со встроенным аккумулятором (к примеру, ноутбуки или портативные устройства), но для большинства остальных источник бесперебойного питания является необходимым.

При установке такого источника можно не только установить негативные последствия потерь, но и уменьшить траты на оплату электричества. Специалисты доказали, что в среднем, ИБП поможет экономить от 20 % до 50 %. Почему это происходит:

1. Значительно уменьшается нагрузка силовых трансформаторов;
2. Провода меньше нагреваются, это не только положительно влияет на их работу, но и повышает безопасность;
3. У сигнальных и радиоустройств уменьшаются помехи;
4. На порядок уменьшаются гармоники в электрической сети.

В некоторых случаях специалисты используют не полноценные ИБП, а специальные компенсирующие конденсаторы. Они подходят для бытового использования, доступны и продаются в каждом электротехническом магазине. Для расчета планируемой и полученной экономии можно использовать все вышеперечисленные формулы.

Источник: https://www.asutpp.ru/aktivnaya-moshhnost-cepi-peremennogo-toka.html

Формула расчета мощности по току и напряжению электросхемы

Пожаловалась бабушка соседка снизу: подарили мне дети моющий пылесос. Он прекрасно работает, но откуда-то идет запах гари.

Пошел смотреть. Проводка у нас старая: лапша из алюминия 2,5 квадрата. А пылесос потребляет 2,5 kW. Прикинул, как работает формула расчета мощности по току и напряжению для этого случая.

Разделил 2500 ватт на 220 вольт. Получил чуть больше 11 ампер. Наши провода держат нагрузку 22 А. Имеем практически двойной резерв по току. Другие потребители при уборке отключены.

Стали проверять и нюхать: запах около квартирного щитка. Открыл, осмотрел: шина сборки ноля в саже, на одной перемычке горелая изоляция. Винт крепления ослаблен. Вот и причина начала возгорания. Исправил.

На этом примере я показываю, что всегда надо оценивать мощность потребления электроприборов и возможности проводки с защитными устройствами. Об этом рассказываю ниже.

Что такое мощность в электричестве: просто о сложном

Вспомнилась былина об Илье Муромце, когда он приложил всю свою мощь к соловью разбойнику. У бедолаги сразу посыпались искры из глаз, как пламя с верхней картинки на проводке с неправильным монтажом.

Простыми словами: мощность в электричестве — это силовая характеристика энергии, которой оценивают, как способности генераторных установок ее вырабатывать, так возможности потребителей и транспортных магистралей.

Все эти участки должны быть точно смонтированы и налажены для обеспечения безопасной работы. Как только в любом месте возникает неисправность, так сразу развивается авария во всей схеме.

1. включенными в сеть приборами;
2. конструкцией проводов и кабелей;
3. настройкой защитных устройств.

Только комплексное решение этих трех вопросов может обеспечить безопасность проводки и жильцов.

Как рассчитать электрическую мощность в быту

Формулы расчета мощности в электричестве позволяют выполнить качественную оценку безопасности каждого из перечисленных выше пунктов.

Пользоваться ими не сложно. Я уже приводил в предыдущих статьях шпаргалку электрика, где они помещены в наглядной форме для цепей постоянного тока.

Они полностью справедливы для активной составляющей мощности переменного тока, совершающей полезную работу. Кстати, кроме нее есть еще и бесполезная — реактивная, связанная с потерями энергии. Ее описанию посвящен второй раздел.

Такие вычисления удобно делать с помощью онлайн калькулятора. Он избавляет от рутинных математических вычислений и арифметических ошибок.

При любом из способов для расчета активной мощности требуется знать две из трех электрических величин:

1. силу тока I;
2. приложенное напряжение U;
3. сопротивление участка цепи R.

Как измерить электрическую мощность дома

Существует еще одна возможность оценки активной мощности: ее измерение в действующей схеме специальными приборами: ваттметрами.

https://www.youtube.com/watch?v=QBPe-8daSOs

Точные замеры может обеспечить промышленный лабораторный ваттметер. Он изготавливается как прибор, работающий на аналоговых сигналах,так и с помощью цифровых технологий.

В бытовой проводке точные вычисления не нужны. Для нее выпускаются различные виды более простых ваттметров.

Популярностью пользуются приборы, которые можно вставить в розетку и подключить к ним шнур питания от потребителя, включить их в работу и сразу снять показания на дисплее в ваттах.

Такие приборы избавляют электрика от выполнения сложных операций под напряжением, когда требуется замерять:

• действующее напряжение;
• силу тока;
• угол сдвига фаз между векторами тока и напряжения.

Потом все данные дополнительно требуется вводить в формулу расчета мощности по току и напряжению, делать по ней вычисления.

Этот метод можно упростить, если внимательно наблюдать за показаниями электрического счетчика индукционной системы с вращающимся диском. Он считает совершенную работу: потребленную мощность за определенную время.

Однако скорость вращения диска как раз и характеризует величину потребления. Надо просто посчитать сколько раз он обернется за минуту и перевести в ватты по табличке, расположенной на корпусе.

Почему реактивное сопротивление схемы влияет на мощность переменного тока

Синусоидальная гармоника напряжения, поступая на резистивное сопротивление, изменяет величину тока без его отклонения на комплексной плоскости.

Такой ток совершает полезную работу с минимальными потерями энергии, вырабатывая активную мощность. Частота колебания сигнала не оказывает на нее никакого влияния.

Сопротивление конденсатора и индуктивности зависит от частоты гармоники. Его противодействие отклоняет направление тока на каждом из этих элементов в разные стороны.

Захотелось его нарисовать на фоне оборудования из нагромождений фарфора и металла, где пришлось поработать довольно долго.Отвлекся. Не судите за это строго.

Сравните его с опубликованным мною ранее треугольником сопротивлений. Находите общие черты?

Ими являются геометрические пропорции фигуры, описывающие их формулы и угол φ, определяющий потери полной мощности. Перехожу к их более подробному рассмотрению.

Формулы расчета мощности для однофазной и трехфазной схемы питания

В идеальном теоретическом случае трехфазная схема состоит из трех одинаковых однофазных цепей. На практике всегда есть какие-то отклонения. Но, в большинстве случаев при анализах ими пренебрегают.

Поэтому рассматриваем вначале наиболее простой вопрос.

Как работает резистор

На чисто резистивном сопротивлении синусоиды тока и напряжения совпадают по углу, направлены на каждом полупериоде одинаково.Поэтому их произведение, выражающее мощность, всегда положительно.

Его значение в произвольный момент времени t называют мгновенным, обозначая строчной буквой p.

Среднее значение мощности в течение одного периода называют активной составляющей. Ее график для переменного тока имеет фигуру симметричного всплеска с максимальным значением Pm в середине каждого полупериода Т/2.

Его площадь равна двум площадям графиков активной составляющих одного любого полупериода. Если посмотреть на картинку внимательнее, то можно представить, что верхняя часть всплеска отрезана,перевернута и заполнила свободное пространство внизу.

Представление этого графика помогает запомнить, что на активном сопротивлении мощность постоянного и переменного тока вычисляется по одной формуле, не меняет своего знака.

График мгновенных значений активной мощности переменного тока на резистивном сопротивлении имеет вид повторяющихся положительных волн. Но за один период им совершается такая же работа, как и в цепях постоянного тока и напряжения.

На резисторе не создается реактивных потерь.

Как работает индуктивность

Катушка с обмоткой своими витками запасает энергию магнитного поля. Благодаря процессу ее накопления индуктивное сопротивление отодвигает вперед на 90 градусов вектор тока относительно приложенного напряжения на комплексной плоскости.

Перемножая их мгновенные величины получаем значения мощности, которое за один период меняет знаки (направление) в каждом полупериоде.

Частота изменения мощности на индуктивности в два раза выше,чем у ее составляющих: синусоид тока и напряжения. Она состоит из двух частей:

1. активной, обозначаемой индексом PL;
2. реактивной QL.

Реактивная часть на индуктивности создается за счет постоянного обмена энергией между катушкой и приложенным источником. На ее величину влияет значение индуктивного сопротивления XL.

Как работает конденсатор

Емкость конденсатора постоянно накапливает заряд между своими обкладками. За счет этого происходит сдвиг вектора тока вперед на 90 градусов относительно приложенного напряжения.

График мгновенной мощности напоминает вид предыдущего, но начинается с отрицательной полуволны.

Реактивная составляющая, выделяемая на конденсаторе, зависит от величины емкостного сопротивления XC.

Как работает реальная схема со всеми видами сопротивлений

В чистом виде приведенные выше графики и выражения встречаются не так часто. На самом деле передача электроэнергии и ее работа на переменном токе связаны с комплексным преодолением сил электрического сопротивления резисторов, конденсаторов и индуктивностей.

Причем, какая-то из этих составляющих будет преобладать. Для таких случаев преобразования электрической энергии в мгновенную мощность могут иметь один из следующих видов.

На верхней картинке показан случай, когда вектор тока отстает от приложенного напряжения, а на нижней — опережает.

В обоих случаях величина активной составляющей уменьшается от значения полной на значение, выражаемое как cosφ. Поэтому его принято называть коэффициентом мощности.

Косинус фи (cosφ) используется при анализе треугольника мощностей и сопротивлений, характеризует потери энергии.

Как работает схема трехфазного электроснабжения

На ввод распределительного щита многоэтажного здания поступает трехфазное напряжение от электроснабжающей организации, вырабатываемое промышленными генераторами.

Его же, за отдельную плату, при желании может подключить владелец частного дома, что многие и делают. При этом рабочая схема и диаграмма напряжений выглядит следующим образом.

В старой системе заземления TN-C она выполняется четырехпроводным подключением, а у новой TN-S — пятипроводным с добавлением защитного РЕ проводника. Его на этой схеме я не показываю для упрощения.

Каждую из фаз при работе необходимо стараться нагружать одинаково равными по величине токами. Тогда в домашней проводке будет создаваться наиболее благоприятный оптимальный режим без опасных перекосов энергии.

А поскольку они все идентичные, то их просто утраивают.

Например, когда активная мощность фазы В имеет выражением Рв=Uв×Iв×cosφ, то для всей трехфазной схемы она будет выражена следующей формулой:

Р = Рa+Рв+Рc

Если пометить фазное выражение буквой ф. например Pф, томожно записать:

P = 3Pф = 3Uф×Iф×cosφ

Аналогично будет вычисляться реактивная составляющая

Q = Qa+Qв+Qc

Или

Q = 3Qф = 3Uф×Iф×sinφ

Поскольку P и Q представляют величины катетов прямоугольного треугольника, то гипотенузу или полную составляющую можно вычислить как квадратный корень из суммы их квадратов.

S = √(P2+Q2)

Как учитывается трехфазная полная мощность

В энергосистеме, да и в частном доме, требуется анализировать подключенные нагрузки, равномерно распределять их по источникам напряжений.

С этой целью работают многочисленные конструкции измерительных приборов. На щитах управления подстанций расположены щитовые ваттметры и варметры, предназначенные для работы в разных долях кратности.

Старые аналоговые приборы показаны на этой картинке.

Для того, чтобы не путаться в записях вычислений введены разные наименования единиц. Они обозначаются:

• ВА — (русское), VA (международное) вольтампер для полной величины мощности;
• Вт —(русское), var (международное) ватт —активной;
• вар (русское), var (международное) — реактивной.

Аналоговые приборы измеряют только активную или реактивную составляющую, а полную величину необходимо вычислять по формулам.

Многие современные цифровые приборы способны осуществлять эту функцию автоматически.

урок Павла Виктор дополняет мой материал. Рекомендую посмотреть.

Калькулятор мощности для своих

Здесь вы можете выполнить вычисления онлайн без использования формул и арифметических действий. Просто введите ваши исходные данные в таблицу и жмите кнопку “Рассчитать ток”.

А в заключение напоминаю, что для ваших вопросов создан раздел комментариев. Задавайте их, я отвечу.

Источник: https://ElectrikBlog.ru/formula_rascheta_moshchnosti_po_toku_i_napryazheniyu_elektroskhemy/

Реактивная мощность

В технической литературе и сопроводительной документации применяют разные обозначения электрических параметров. Реактивная мощность определяет часть процессов при подключении индуктивных (емкостных) нагрузок. Вместе с активной (рабочей) составляющей она формирует полные энергетические характеристики цепи переменного тока.

Наглядная демонстрация физических понятий

Мощность активная, реактивная и полная

Перечисленные понятия рассматривают с учетом особенностей нагрузки. Активная мощность потребляется обычным проводником. При увеличении силы тока энергия расходуется на повышение температуры (ТЭН чайника) или световое излучение (нить лампы накаливания).

Индуктивная нагрузка и конденсатор потребляют реактивную мощность. Энергия в этих вариантах преобразуется в магнитное (электрическое) поле, соответственно. Суммарная величина – полная мощность.

Смысл реактивной нагрузки

Любая реактивная нагрузка создает временной сдвиг между фазами тока и напряжения. Эту величину измеряют в градусах. Наиболее наглядным является векторное представление электрических параметров. Если подключить индуктивность, напряжение будет опережать ток. Угол между ними обозначают в формулах буквой «ϕ» («Фи» греч.).

Временные и векторные диаграммы показывают, как изменяются основные параметры при подключении индуктивных (емкостных) элементов

На картинке показано, что при подключении емкостной нагрузки вектора «меняются» местами. В идеальных условиях сдвиг между векторами равен 90°. В действительности следует учитывать влияние электрического сопротивления цепи, несовершенство конструкций. С учетом особенностей элементов следует напомнить, что в индуктивности (емкости) при сохранении параметров источника питания плавно изменяется ток (напряжение), соответственно.

Почему в сети напряжение переменное

Для объяснения настоящей ситуации надо сделать краткий экскурс в историю. Электричество известно человеку сотни (по некоторым данным, тысячи лет). Однако действительно массовое использование этой энергии началось сравнительно недавно – в конце 19 века. Именно тогда (1879 г.) Эдисон запатентовал первый функциональный прибор, который помогал решать проблемы освещения. Для питания лампочек он стал монтировать сети постоянного тока.

Через десять лет Тесла создал генераторы переменного тока. После ожесточенной конкурентной борьбы именно его способ передачи энергии на расстояния одержал победу. Этот результат был обеспечен скорее рыночными методами, чем внимательным сравнением потребительских характеристик.

К сведению. Метрополитен Нью-Йорка до сих пор функционирует с подключением к сети постоянного тока.

Выгода от переменного напряжения

Важные для потребителей преимущества этого варианта приведены в следующем перечне:

• простая конструкция генераторов/ электродвигателей;
• минимальные потери при передаче электроэнергии на сравнительно небольшие расстояния;
• простота преобразования напряжения с применением трансформатора;
• поддержание стабильности оборотов электрических приводов без лишних трудностей;
• отсутствие полярности.

Каждый из пунктов можно рассмотреть подробно. Генератор (электромотор) переменного тока, например, нетрудно создать без токосъемных щеток и постоянных магнитов. Простота конструкции обеспечивает:

• разумную стоимость;
• минимальные затраты при обслуживании и ремонте;
• долговечность;
• надежность.

Обороты мощных электродвигателей регулируют изменением частоты. Это значит, что в обычных условиях эксплуатации обеспечивается поддержание расчетных параметров без дополнительных схем управления и контроля. В частности, отмеченные особенности идеально подходят для создания насосной станции.

Для повышения/ уменьшения напряжения в сетях переменного тока используют типовые сравнительно недорогие конструкции. Изменяя количество витков обмотки на едином сердечнике, можно получить необходимый коэффициент трансформации с высокой точностью. В процессе работы дополнительная настройка не требуется.

Постоянное напряжение снижают с применением электрического сопротивления, которое в данном случае не выполняет никаких полезных функций. Для повышения – применяют сложные схемы с промежуточным преобразованием в переменный сигнал.

Какой из способов предпочтительнее, можно определить после перечисления преимуществ сетей постоянного тока:

• возможность подключения непосредственно к источнику питания светодиодов, гальванических ванн, иных потребителей;
• простая зарядка аккумуляторных батарей;
• отсутствие необходимости согласования нагрузок;
• высокая точность измерений;
• минимальные потери при передаче электроэнергии на большие расстояния;
• применение «однопроводной» линии питания (метро, трамвай).

Убытки от переменного напряжения

Формулы расчетов активной и реактивной мощностей подробно рассмотрены в следующих разделах статьи. Однако для изучения потерь в сетях переменного тока необходимо привести определение поправочного коэффициента cosϕ (косинус Фи). Это значение производители указывают в технических паспортах и на бирках корпусов мощных моторов, сварочных аппаратов, другой техники.

Потери в электрической схеме а) с диаграммой полной б) и частичной в) компенсации

В этом примере рассмотрена приближенная к реальной ситуация, когда подключены активные нагрузки вместе с реактивными. Если cosϕ=0,75, то при одной и той же потребляемой мощности номинальный ток в цепи (100 А) увеличится следующим образом:

I = Ia/ cosϕ = 100/0,75 ≈ 133 А.

При этом на повышение температуры будет расходоваться мощность, пропорциональная квадрату тока. Считать ее можно по формуле:

Pнагр = I2 * Rc.

Соответствующие потери увеличатся в 1,77 раза.

Следует отметить! Изменения силы тока сопровождаются колебаниями напряжения. Иные потребители, подключенные к этой же сети, будут работать в неблагоприятных режимах. При этом счетчик будет показывать неизменное потребление энергетических ресурсов.

Понятной является ситуация, когда ИБП или другой источник питания начинает выдавать ток, превышающий расчетные параметры. Перегревается не только генератор, но и проводка. Значительно возрастает риск аварий, поломок.

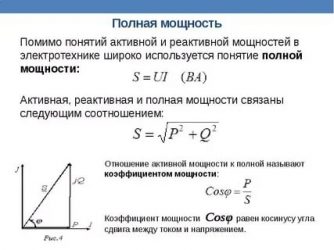
Активная, реактивная и полная мощности в формулах

Чтобы рассчитать или измерить мощность: полную, активную и реактивную, служат основные формулы:

• активная мощность = полная * cosϕ;
• реактивная = напряжение * ток * sinϕ.

Для упрощения можно начать с примера на основе цепи постоянного тока, где действительна известная формула:

Pa = U * I.

Это активная (рабочая, полная) мощность. Единицы измерения – ватт (Вт), киловатт (кВт), другие производные. При подключении сопротивления (R) ее можно вычислить следующим образом:

• Pa = I2 * R;
• Pa = U2 / R.

Простота исчезает при рассмотрении сигналов синусоидальной формы. Именно такими параметрами отличаются стандартные сети питания (220/380V). Активная мощность в этом случае зависит от фазового сдвига между векторами тока и напряжения.

Соответствующие зависимости выражают следующим образом:

Pa = U * I * cosϕ.

Эта формула подходит для расчета обычной сети 220V, которой пользуется большинство рядовых потребителей. Мощные насосы и станки подключают к трехфазным источникам питания 380 V. Для этого варианта нужна коррекция:

Pa = √3 * U * I * cosϕ = 1,732 * U * I * cosϕ.

Реактивная мощность (Pq) не только потребляется нагрузкой, но и возвращается обратно в источник питания. Ее значение определяют следующим образом:

Pq = U * I * sinϕ.

К сведению. Измеряется эта величина в реактивных вольт-амперах (вар).

Для вычисления полной мощности формула содержит перечисленные выше компоненты:

Ps = √( Pa2 + Pq2).

Что такое реактивная мощность

Эту мощность можно назвать бесполезной, так как она обозначает переход энергии между источником питания и нагрузкой. Недоступный для практического применения энергетический потенциал в данном случае только увеличивает потери.

Треугольник мощностей

На картинке ниже рядом с электрической схемой приведены графические изображения мощностей. Соответствующими векторами обозначены мощности:

• S – полная;
• Q – реактивная;
• P – активная.

Коэффициент мощности

Этим термином обозначают потери, созданные реактивной нагрузкой. Обозначение – cosϕ.

Коррекция cos ϕ

Для компенсации угла сдвига фаз используют дополнительные электрические компоненты. При индуктивном характере нагрузки подключают параллельно конденсатор. Емкость рассчитывают по формуле:

C=I/(w*U), где w – угловая частота.

Как и где измеряют cos ϕ

Потери определяют по изменению силы тока, напряжения и мощности в цепях с мощными реактивными нагрузками:

cosϕ = P/ (I * U).

Можно найти в магазине либо арендовать специализированный прибор –  «фазометр». Специализированные сервисы предлагают расчет электрических параметров онлайн.

Колебательный процесс в цепях переменного тока сопровождается изменением магнитного (электрического) поля для индуктивной и емкостной нагрузки, соответственно.

Электроприборы, влияющие на качество потребления

Как перевести ватты в амперы

Коэффициент мощности равен единице при подключении ламп и нагревателей. Он уменьшается до 0,7 и менее, когда в цепи добавляют преобладающие по потреблению энергии электромоторы, другие компоненты с реактивными составляющими.

Правильное применение определений и расчетов мощности помогает оптимизировать проект электрической сети с учетом особенностей подключаемых нагрузок. Приведенные выше сведения пригодятся на стадии определения параметров проводки, защитных автоматов. Комплексное использование этих знаний повысит надежность электроснабжения, предотвратит возникновение и развитие аварийных ситуаций.

Источник: https://amperof.ru/teoriya/reaktivnaya-moshhnost.html

Активное сопротивление в цепи переменного тока

Электрические лампы накаливания, печи сопротивления, бытовые нагревательные приборы, реостаты и другие приемники, где электрическая энергия преобразуется в тепловую, на схемах замещения обычно представлены только сопротивлением R.
Для схемы, изображенной на рис. 13.1, а, заданы сопротивление R и напряжение, изменяющееся по закону

u = Umsinωt

Найдём ток и мощность в цепи.

Ток в цепи переменного тока с активным сопротивлением

По закону Ома найдем выражение для мгновенного тока:

где Im = Um/R — амплитуда тока

Из уравнений напряжения и тока видно, что начальные фазы обеих кривых одинаковы, т. е. напряжение и ток в цепи с сопротивлением R совпадают по фазе. Это показано на графиках и векторной диаграмме (рис. 13.1, б, б).

Действующий ток найдем, разделив амплитуду на √ 2:

Формулы (13.1) выражают закон Ома для цепи переменного тока с сопротивлением R. Внешне они ничем не отличаются от формулы для цепи постоянного тока, если переменные напряжение и ток выражены действующими величинами.

 Мгновенная мощность в цепи переменного тока с активным сопротивлением

При переменных величинах напряжения и тока скорость преобразования электрической энергии в приемнике, т. е. его мощность, тоже изменяется. Мгновенная мощность равна произведению мгновенных величин напряжения и тока: p  = Umsinωt * Imsinωt = UmImsin2ωt

Из тригонометрии найдём 

Более наглядное представление о характере изменения мощности в цепи дает график в прямоугольной системе координат, который строится после умножения ординат кривых напряжения и тока, соответствующих ряду значений их общего аргумента — времени t. Зависимость мощности от времени — периодическая кривая (рис. 13.2). Если ось времени t поднять по чертежу на величину р = Pm√2 = UmIm√2, то относительно новой оси t’ график мощности является синусоидой с двойной частотой и начальной фазой 90°:

Таким образом, в первоначальной системе координат мгновенная, мощность равна сумме постоянной величины Р= UmIm√2 и перемен- ной р’:

р = Р + р’

Анализируя график мгновенной мощности, нетрудно заметить, что мощность в течение периода остается положительной, хотя ток и напряжение меняют свой знак. Это получается благодаря совпадению по фазе напряжения и тока.

Постоянство знака мощности говорит о том, что направление потока электрической энергии остается в течение периода неизменным, в данном случае от сети (от источника энергии) в приемник с сопротивлением R, где электрическая энергия необратимо преобразуется в другой вид энергии. В этом случае электрическая энергия называется активной.

Если R — сопротивление проводника, то в соответствии с законом Ленца — Джоуля электрическая энергия в нем преобразуется в тепло.

Активная мощность для цепи переменного тока с активным сопротивлением

Скорость преобразования электрической энергии в другой вид энергии за конечный промежуток времени, значительно больший периода изменения тока, характеризуется средней мощностью. Она равна средней мощности за период, которую называют активной.

Активная мощность — среднее арифметическое мгновенной мощности за период.

Для рассматриваемой цепи активную мощность Р нетрудно определить из графика рис. 13.2. Средняя величина мощности равна высоте прямоугольника с основанием Т, равновеликого площади, ограниченной кривой р(t) и осью абсцисс (на рисунке заштриховано).

Равенство площадей РТ = Sp выполняется, если высоту прямоугольника взять равной половине наибольшей мгновенной мощности Pm.

P = UI

Активная мощность для данной цепи равна произведению действующих величин тока и напряжения:

P = UI = I2R = U2R

С математической точки зрения активная мощность является постоянной составляющей в уравнении мгновенной мощности p(t) [см. выражение (13.2)].

Среднюю мощность за период можно найти интегрированием уравнения (13.2) в пределах периода:

Сопротивление R, определяемое из формулы (13.3) отношением активной мощности цепи к квадрату действующего тока, называется активным электрическим сопротивлением.

Источник: https://electrikam.com/aktivnoe-soprotivlenie-v-cepi-peremennogo-toka/

Что такое активная, реактивная и полная мощность — простое объяснение

Простое объяснение понятий активная, реактивная и полная мощность. В чем отличие этих мощностей и как их рассчитать.

В цепях постоянного тока не разделяют мощность на разные составляющие, такие как активная и реактивная, поэтому используют простое выражение P=U*I. Но с переменным током дело обстоит иначе. В этой статье мы рассмотрим, что такое активная, реактивная и полная мощность электрической цепи.

Смысл реактивной нагрузки

В электрической цепи с реактивной нагрузки фаза тока и фаза напряжения не совпадают во времени. В зависимости от характера подключенного оборудования напряжение либо опережает ток (в индуктивности), либо отстаёт от него (в ёмкости). Для описания вопросов используют векторные диаграммы. Здесь одинаковое направление вектора напряжения и тока указывает на совпадение фаз. А если вектора изображены под некоторым углом, то это и есть опережение или отставание фазы соответствующего вектора (напряжения или тока). Давайте рассмотрим каждый из них.

В индуктивности напряжение всегда опережает ток. «Расстояние» между фазами измеряется в градусах, что наглядно иллюстрируется на векторных диаграммах. Угол между векторами обозначается греческой буквой «Фи».

В идеализированной индуктивности угол сдвига фаз равен 90 градусов. Но в реальности это определяется полной нагрузкой в цепи, а в реальности не обходится без резистивной (активной) составляющей и паразитной (в этом случае) емкостной.

В ёмкости ситуация противоположна – ток опережает напряжение, потому что индуктивность заряжаясь потребляет большой ток, который уменьшается по мере заряда. Хотя чаще говорят, что напряжение отстаёт от тока.

Если сказать кратко и понятно, то эти сдвиги можно объяснить законами коммутации, согласно которым в ёмкости напряжение не может изменится мгновенно, а в индуктивности – ток.

Треугольник мощностей и косинус Фи

Если взять всю цепь, проанализировать её состав, фазы токов и напряжений, затем построить векторную диаграмму. После этого изобразить активную по горизонтальной оси, а реактивную – по вертикальной и соединить результирующим вектором концы этих векторов – получится треугольник мощностей.

Он выражает отношение активной и реактивной мощности, а вектор, соединяющий концы двух предыдущих векторов – будет выражать полную мощность. Всё это звучит слишком сухо и запутано, поэтому посмотрите на рисунок ниже:

Буквой P – обозначена активная мощность, Q – реактивная, S – полная.

Формула полной мощности имеет вид:

Самые внимательные читатели наверняка заметили подобие формулы теореме Пифагора.

Единицы измерения:

• P – Вт, кВт (Ватты);
• Q – ВАр, кВАр (Вольт-амперы реактивные);
• S – ВА (Вольт-амперы);

Расчёты

Для вычисления полной мощности используют формулу в комплексной форме. Например, для генератора расчет имеет вид:

А для потребителя:

Но применим знания на практике и разберемся как рассчитать потребляемую мощность. Как известно мы, обычные потребители, оплачиваем только за потребление активной составляющей электроэнергии:

P=S*cosФ

Здесь мы видим, новую величину cosФ. Это коэффициент мощности, где Ф – это угол между активной и полной составляющей из треугольника. Тогда:

cosФ=P/S

В свою очередь реактивная мощность рассчитывается по формуле:

Q = U*I*sinФ

Всё вышесказанное справедливо и для трёхфазной цепи, отличаться будут только формулы.

Ответы на популярные вопросы

Полная, активная и реактивная мощности являются важной темой в электричестве для любого электрика. В качестве заключения мы сделали подборку из 4 часто задаваемых вопросов на этот счёт.

• Какую работу выполняет реактивная мощность?

Ответ: полезной работы не выполняет, но нагрузкой на линии является полная мощность, в том числе с учетом реактивной составляющей. Поэтому чтобы снизить общую нагрузку с ней борются или говоря грамотным языком компенсируют.

— В этих целях используют установки для компенсации реактива. Это могут быть конденсаторные установки или синхронные компенсаторы (синхронные электродвигатели). Подробнее мы рассматривали этот вопрос в статье: https://samelectrik.ru/kompensaciya-reaktivnoj-moshhnosti.html

• Из-за каких потребителей возникает реактив?

— Это в первую очередь электродвигатели – самый многочисленный вид электрооборудования на предприятиях.

• Чем вредит большое потребление реактивной энергии?

— Кроме нагрузки на линии электропередач следует учитывать, что предприятия оплачивает полную мощность, а физические лица – только активную. Это приводит к повышенной сумме оплаты за электроэнергию.

На видео предоставлено простое объяснение понятий реактивной, активной и полной мощностей:

На этом мы и заканчиваем рассмотрение данного вопроса. Надеемся, теперь вам стало понятно, что такое активная, реактивная и полная мощность, какие между ними отличия и как определяется каждая величина.

Материалы по теме:

• Для чего нужен ограничитель мощности
• Фазное и линейное напряжение в трехфазных цепях
• Как определить потребляемую мощность электроприборов

Нравится0)Не нравится0)

Источник: https://elektrik-sam.ru/baza-znanij/3531-chto-takoe-aktivnaja-reaktivnaja-i-polnaja-moschnost-prostoe-objasnenie.html

Теория реактивной мощности

Теория реактивной мощности

Появление термина «реактивная» мощность связано с необходимостью выделения мощности, потребляемой нагрузкой, составляющей, которая формирует электромагнитные поля и обеспечивает вращающий момент двигателя. Эта составляющая имеет место при индуктивном характере нагрузки. Например, при подключении электродвигателей. Практически вся бытовая нагрузка, не говоря о промышленном производстве, в той или иной степени имеет индуктивный характер.

В электрических цепях, когда нагрузка имеет активный (резистивный) характер, протекающий ток синфазен (не опережает и не запаздывает) от напряжения. Если нагрузка имеет индуктивный характер (двигатели, трансформаторы на холостом ходу), ток отстает от напряжения. Когда нагрузка имеет емкостной характер (конденсаторы), ток опережает напряжение.

Суммарный ток, потребляемый двигателем, определяется векторной суммой:

1. Iа — активный ток
2. Iри — реактивный ток индуктивного характера

К этим токам привязаны мощности потребляемые двигателем.

1. Р – активная мощность привязана к Iа (по всем гармоникам суммарно)
2. Q – реактивная мощность привязана к Iри (по всем гармоникам суммарно)
3. A – полная мощность потребляемая двигателем. (по всем гармоникам суммарно)

Реактивная мощность не производит механической работы, хотя она и необходима для работы двигателя, поэтому ее необходимо получать на месте, чтобы не потреблять ее от энергоснабжающей организации. Тем самым мы снижаем нагрузку на провода и кабели, повышаем напряжение на клеммах двигателя, снижаем платежи за реактивную мощность, имеем возможность подключить дополнительные станки за счет снижения тока потребляемого с силового трансформатора.

Параметр определяющий потребление реактивной мощности называется Cos (φ)

Cos (φ) = P1гарм / A1гарм

где:

• P1гарм — активная мощность первой гармоники 50 Гц
• A1гарм — полная мощность первой гармоники 50 Гц

где:

A = √P² + Q²

Таким образом, сos (φ) уменьшается, когда потребление реактивной мощности нагрузкой увеличивается. Необходимо стремиться к повышению сos (φ), т.к. низкий сos (φ) несет следующие проблемы:

1. Высокие потери мощности в электрических линиях (протекание тока реактивной мощности);
2. Высокие перепады напряжения в электрических линиях (например 330…370 В, вместо 380 В);
3. Необходимость увеличения габаритной мощности генераторов, сечения кабелей, мощности силовых трансформаторов.

Из всего вышеприведенного, понятно, что компенсация реактивной мощности необходима. Чего легко можно достичь применением активных компенсирующих установок. Конденсаторы в которых будут компенсировать реактивную мощность двигателей.

Потребители реактивной мощности

Потребителями реактивной мощности, необходимой для создания магнитных полей, являются как отдельные звенья электропередачи (трансформаторы, линии, реакторы), так и такие электроприёмники, преобразующие электроэнергию в другой вид энергии которые по принципу своего действия используют магнитное поле (асинхронные двигатели, индукционные печи и т.п.). До 80-85% всей реактивной мощности, связанной с образованием магнитных полей, потребляют асинхронные двигатели и трансформаторы. Относительно небольшая часть в общем балансе реактивной мощности приходится на долю прочих её потребителей, например на индукционные печи, сварочные трансформаторы, преобразовательные установки, люминисцентное освещение и т.п.

Трансформатор как потребитель реактивной мощности. Трансформатор является одним из основных звеньев в передаче электроэнергии от электростанции до потребителя. В зависимости от расстояния между электростанцией и потребителем и от схемы передачи электроэнергии число ступеней трансформации лежит в пределах от двух до шести.

Поэтому установленная трансформаторная мощность обычно в несколько раз превышает суммарную мощность генераторов энергосистемы. Каждый трансформатор сам является потребителем реактивной мощности.

Реактивная мощность необходима для создания переменного магнитного потока, при помощи которого энергия из одной обмотки трансформатора передаётся в другую.

Асинхронный двигатель как потребитель реактивной мощности. Асинхронные двигатели наряду с активной мощностью потребляют до 60-65% всей реактивной мощности нагрузок энергосистемы. По принципу действия асинхронный двигатель подобен трансформатору. Как и в трансформаторе, энергия первичной обмотки двигателя – статора передаётся во вторичную – ротор посредствам магнитного поля.

Индукционные печи как потребители реактивной мощности. К крупным электроприемникам, требующим для своего действия большой реактивной мощности, прежде всего, относятся индукционные печи промышленной частоты для плавки металлов. По существу эти печи представляют собой мощные, но не совершенные с точки зрения трансформаторостроения трансформаторы, вторичной обмоткой которых является металл (садка), расплавляемый индуктированными в нём токами.

Преобразовательные установки, преобразующие переменный ток в постоянный при помощи выпрямителей, также относятся к крупным потребителям реактивной мощности. Выпрямительные установки нашли широкое применение в промышленности и на транспорте. Так, установки большей мощности с ртутными преобразователями используются для питания электроизоляционных ванн, например при производстве алюминия, каустической соды и др. Железнодорожный транспорт в нашей стране почти полностью электрифицирован, причём значительная часть железных дорог использует постоянный ток преобразовательных установок.

Компенсация реактивной мощности в электрических сетях

С другой стороны, элементы распределительной сети (линии электропередачи, повышающие и понижающие трансформаторы) в силу особенностей конструктивного исполнения имеют продольное индуктивное сопротивление. Поэтому, даже для нагрузки потребляющей только активную мощность, в начале распределительной сети будет иметь место индуктивная составляющая – реактивная мощность. Величина этой реактивной мощности зависит от индуктивного сопротивления распределительной сети и полностью расходуется на потери в элементах этой распределительной сети.

Действительно, для простейшей схемы:

• Р – активная мощность в центре питания,
• Рн – активная мощность на шинах потребителя,
• R – активное сопротивление распределительной сети,
• Q – реактивная мощность в центре питания,
• Qн – реактивная мощность на шинах потребителя.
• U – напряжение в центре питания,
• Uн – напряжение на шинах потребителя,
• Х – индуктивное сопротивление распределительной сети.

В результате, независимо от характера нагрузки, по распределительной сети от источника питания будет передаваться реактивная мощность Q. При двигательном характере нагрузки ситуация ухудшается – значения мощности в центре питания увеличивается и становится равными:

Р = Рн + ( Рн² + Qн² ) * R / Uн²;

Q = Qн + ( Рн² + Qн² ) * X / Uн².

Передаваемая от источника питания к потребителю реактивная мощность имеет следующие недостатки:

1. В распределительной сети возникают дополнительные потери активной мощности – потери при транспорте электрической энергии:

   δР = ( Рн² + Qн² ) * R ,

   часть которых (а иногда и значительную) составляют потери от транспорта реактивной мощности.

2. Величина напряжения у потребителя, а, следовательно, и качество электрической энергии, снижается:

   Uн = U – ( P * R + Q * X ) / U.

3. Увеличивается загрузка распределительной сети током, что лишает потребителя возможности перспективного развития.

Таким образом, транспортировка реактивной мощности по распределительным сетям от центров питания к потребителям превращается в сложную технико-экономическую проблему, затрагивающую как вопросы экономичности так и вопросы надежности систем электроснабжения.

Классическим решением данной проблемы в распределительных сетях является компенсация реактивной мощности у потребителя путём установки у него дополнительных источников реактивной мощности – потребительских статических конденсаторов.

Компенсация реактивной мощности применяется:

• по условию баланса реактивной мощности;
• как важное мероприятие для снижения потерь электрической энергии в сетях;
• для регулирования напряжения.

Источник: https://www.nucon.ru/reactive-power/theory-of-reactive-power.php