Как найти u общее в цепи?

Конспект

В предыдущем конспекте «Электрическое сопротивление» был установлено, что сила тока в проводнике зависит от напряжения на его концах. Если в опыте менять проводники, оставляя напряжение на них неизменным, то можно показать, что при постоянном напряжении на концах проводника сила тока обратно пропорциональна его сопротивлению. Объединив зависимость силы тока от напряжения и его зависимость от сопротивления проводника, можно записать: I = U/R. Этот закон, установленный экспериментально, называется закон Ома (для участка цепи).

Закон Ома для участка цепи: сила тока в проводнике прямо пропорциональна приложенному к его концам напряжению и обратно пропорциональна сопротивлению проводника. Прежде всего закон всегда верен для твёрдых и жидких металлических проводников. А также для некоторых других веществ (как правило, твёрдых или жидких).

Потребители электрической энергии (лампочки, резисторы и пр.) могут по-разному соединяться друг с другом в электрической цепи. Два основных типа соединения проводников: последовательное и параллельное. А также есть еще два соединения, которые являются редкими: смешанное и мостовое.

Последовательное соединение проводников

При последовательном соединении проводников конец одного проводника соединится с началом другого проводника, а его конец — с началом третьего и т.д. Например, соединение электрических лампочек в ёлочной гирлянде.  При последовательном соединении проводников ток проходит через все лампочки. При этом через поперечное сечение каждого проводника в единицу времени проходит одинаковый заряд. То есть заряд не скапливается ни в какой части проводника.

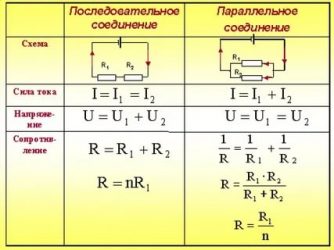
Поэтому при последовательном соединении проводников сила тока в любом участке цепи одинакова: I1 = I2 = I.

Общее сопротивление последовательно соединённых проводников равно сумме их сопротивлений: R1 + R2 = R. Потому что при последовательном соединении проводников их общая длина увеличивается. Она больше, чем длина каждого отдельного проводника, соответственно увеличивается и сопротивление проводников.

Из приведённых равенств следует, что последовательное соединение проводников используется в том случае, если напряжение, на которое рассчитаны потребители электрической энергии, меньше общего напряжения в цепи.

Для последовательного соединения проводников справедливы законы: 

1) сила тока во всех проводниках одинакова; 2) напряжение на всём соединении равно сумме напряжений на отдельных проводниках; 3) сопротивление всего соединения равно сумме сопротивлений отдельных проводников.

Параллельное соединение проводников

Примером параллельного соединения проводников служит соединение потребителей электрической энергии в квартире. Так, электрические лампочки, чайник, утюг и пр. включаются параллельно.

При параллельном соединении проводников все проводники одним своим концом присоединяются к одной точке цепи. А вторым концом к другой точке цепи. Вольтметр, подключенный к этим точкам, покажет напряжение и на проводнике 1, и на проводнике 2. В таком случае напряжение на концах всех параллельно соединённых проводников одно и то же: U1 = U2 = U.

При параллельном соединении проводников электрическая цепь разветвляется. Поэтому часть общего заряда проходит через один проводник, а часть — через другой. Следовательно при параллельном соединении проводников сила тока в неразветвлённой части цепи равна сумме силы тока в отдельных проводниках: I = I1 + I2.

В соответствии с законом Ома   I = U/R,   I1 = U1/R1,   I2 = U2/R2. Отсюда следует: U/R = U1/R1 + U2/R2, U = U1 = U2,  1/R = 1/R1 + 1/R2  Величина, обратная общему сопротивлению параллельно соединенных проводников, равна сумме величин, обратных сопротивлению каждого проводника.

При параллельном соединении проводников их общее сопротивление меньше, чем сопротивление каждого проводника. Действительно, если параллельно соединены два проводника, имеющие одинаковое сопротивление г, то их общее сопротивление равно: R = г/2. Это объясняется тем, что при параллельном соединении проводников как бы увеличивается площадь их поперечного сечения. В результате уменьшается сопротивление.

Из приведённых формул понятно, почему потребители электрической энергии включаются параллельно. Они все рассчитаны на определённое одинаковое напряжение, которое в квартирах равно 220 В. Зная сопротивление каждого потребителя, можно рассчитать силу тока в каждом из них. А также соответствие суммарной силы тока предельно допустимой силе тока.

Для параллельного соединения проводников справедливы законы:

1) напряжение на всех проводниках одинаково; 2) сила тока в месте соединения проводников равна сумме токов в отдельных проводниках; 3) величина, обратная сопротивлению всего соединения, равна сумме величин, обратных сопротивлениям отдельных проводников.

Смешанное соединение проводников

Смешанное соединение – соединение, которое является совокупностью последовательных и параллельных соединений. Для нахождения эквивалентного сопротивления нужно, “свернуть” схему поочередным преобразованием параллельных и последовательных участков цепи.

Существует и 4-й вид соединения проводников — мостовое, которое является самым сложным.

Конспект урока по физике в 8 классе «Закон Ома. Соединение проводников».

Следующая тема: «Работа и мощность электрического тока».

Источник: https://uchitel.pro/%D0%B7%D0%B0%D0%BA%D0%BE%D0%BD-%D0%BE%D0%BC%D0%B0-%D1%81%D0%BE%D0%B5%D0%B4%D0%B8%D0%BD%D0%B5%D0%BD%D0%B8%D0%B5-%D0%BF%D1%80%D0%BE%D0%B2%D0%BE%D0%B4%D0%BD%D0%B8%D0%BA%D0%BE%D0%B2/

Параллельное и последовательное соединение проводников в электрической цепи

При монтаже электрических цепей в электротехнике применяют последовательное и параллельное соединение проводников. От выбранного способа соединения источников и потребителей в значительной мере зависят рабочие параметры подключенного оборудования. Поэтому особенности обоих методов построения схемы обязательно должны учитываться при проектировании электроцепей.

Что такое параллельное соединение проводников

При данном способе в составе схемы в крайних точках соединяются начала и концы всех нагрузок, подключенных к источнику электротока. Сами же нагрузки размещаются параллельно по отношению друг к другу. Количество подключенных по такой схеме компонентов не ограничивается. Схема используется во многих сферах, позволяя решать разные задачи компоновки сетей. Например, часто задействуют параллельное соединение аккумуляторов.

При контрольном измерении значения вольтажа электроприборов вольтметр будет показывать одинаковые величины. Это означает, что электронапряжение на каждой нагрузке будет равняться общей величине вольтажа, действующего в электрической цепи.

Особенностью схемы параллельного соединения можно назвать разветвление цепи. В месте разветвления происходит деление заряда с направлением его частей по отдельной линии к соответствующему проводнику. Поэтому общая величина тока будет равна суммарному значению токов на каждой из включенных нагрузок.

Совокупное электрическое сопротивление всей электроцепи имеет меньшее абсолютное значение, по сравнению с каждым из приборов.

Что такое последовательное соединение проводников

Суть этого способа заключается в том, что компоненты цепи подключаются друг к другу поочередно. Первый проводник одним проводом подключается к источнику питания. Второй его провод соединяется со вторым проводником, от которого идет конец на третий проводник и т.д., пока цепь не будет замкнута. Классическим примером последовательной электроцепи можно назвать подключение лампочек в гирлянде.

Ток проходит по цепи приборов, состоящей из резисторов, ламп или других нагрузок, протекая через каждый включенный в электроцепь прибор. В собранной таким способом цепи отсутствует эффект деления и накопления заряда на разных ее участках. Соответственно, физическая величина ампеража будет на всех участках одинаковой.

Совокупное электросопротивление всех последовательно соединенных нагрузок, приборов и устройств любого типа равняется сумме их индивидуальных сопротивлений. Таким образом, его значение прямо зависит от количества подключенных приборов и их параметров.

Аналогично рассчитывается и совокупный вольтаж. Он равняется сумме напряжений, действующих на каждом отдельном электроприборе.

Разница между последовательным и параллельным соединением, преимущества и недостатки

Принципиальные отличия между последовательным и параллельным соединение проводников по ключевым электротехническим параметрам приведены в таблице:

Параметр/тип соединения	Последовательное	Параллельное
Электросопротивление	Равняется сумме электросопротивлений всех электропотребителей.	Меньше значения электросопротивления каждого отдельного из подключенных электроприборов.
Напряжение	Равняется совокупному вольтажу всех электропотребителей.	Одинаковая величина на всех участках электроцепи.
Сила тока	Одинаковая величина на всех участках электроцепи.	Равняется совокупному значению токов на каждом из приборов.

Плюсы и минусы последовательного соединения

Основными преимуществам электроцепей из последовательно соединенных приборов являются их следующие особенности:

• простота проектирования и построения схемы;
• низкая стоимость комплектации;
• возможность подключения приборов, рассчитанных на меньшее рабочее напряжение, по сравнению с номинальным напряжением сети;
• выполнение функции регулирования тока – обеспечивает равномерные нагрузки на все приборы.

Однако у этого способа компоновки электросхемы есть и серьезные недостатки. Главным из них является ненадежность цепи из последовательно соединенных проводников. При выходе из строя любого из подключенных приборов, происходит отключение всей цепи.

Кроме того, минусом является снижение напряжения при увеличении количества подключенных потребителей. Примером может служить последовательное соединение нескольких ламп. Чем больше осветительных приборов подключено таким способом к источнику электропитания, тем менее яркий свет они будут давать.

Плюсы и минусы параллельного соединения

При использовании параллельного соединения проводников обеспечиваются такой набор преимуществ:

• стабильность напряжения на электроприборах, вне зависимости от их числа;
• возможность включения или отключения отдельных участков в нужный момент без нарушения работы всей электроцепи;
• надежность – при выходе одного или нескольких компонентов из строя сама электроцепь продолжает сохранять работоспособность.

Недостатком является более сложный расчет и сложная схема, использование которой повышает стоимость комплектации электросети.

Не допускается подключение приборов, с номинальным рабочим вольтажом меньше сетевого. Параллельное соединение аккумуляторов с разным значением вольтажа связано с перетеканием тока в АКБ с меньшей его величиной, что может вызывать ускоренный износ батареи.

Закон Ома для участка цепи

Одним из ключевых электротехнических законов можно назвать закон Ома для участка цепи. Именно этим законом объясняются отличия, которые существуют для параллельного и последовательного соединения проводников.

Формулируется он таким образом:

Сила тока в проводнике прямо пропорциональна приложенному к его концам напряжению и обратно пропорциональна сопротивлению проводника.

Записывается он следующей формулой:

I = U/R, где

I – сила тока, (А);

U – вольтаж, (В);

R – электросопротивление, (Ом).

Смешанное соединение проводников в электрической цепи

На практике сборку электроцепей, как правило, проводят таким метод, который предусматривает смешанное соединение проводников. Это комбинированное решение, которое сочетает оба способа. Обычно для монтажа основной сети используют параллель, а отдельные потребители при необходимости объединяют в последовательную сеть.

При расчете и сборке смешанных соединений сопротивлений обязательно должны учитываться особенности, преимущества и недостатки обоих методов подключения. В ходе проектирования, схему целесообразно разбить на отдельные части и выполнить расчет в по физическим законам, которые справедливы для последовательного и параллельного соединения. После этого, составные части объединяют в единую схему.

Как соединить вольтметр и амперметр в цепь

К числу основных электротехнических параметров относятся сила тока и вольтаж. Для контроля этих величин используют приборы – амперметры и вольтметры. Требования по подключению этих приборов в цепь определяются, исходя из законов, которые действуют для последовательного и параллельного соединения.

Для измерения величины тока производится включение амперметра в цепь строго последовательно с рабочей нагрузкой. Важно, чтобы сопротивление самого прибора было минимальным, чтобы не допустить его влияние на работу электрооборудования. Если амперметр подключить параллельно, это приведет к выходу амперметра из строя.

Для измерения напряжения вольтметр в цепь подключается строго параллельно источнику или приемнику тока. Сам измерительный прибор должен иметь довольно высокое собственное сопротивление. Это требуется, чтобы при измерении можно было пренебречь величиной тока, который отбирается через вольтметр.

Применение параллельного и последовательного соединения в электротехнике

Параллельное соединение активно применяется для монтажа проводки и цепей в различных видах электрического оборудования и приборов. Оно дает возможность подключить электрические устройства к электросети независимо друг от друга.

Последовательное соединение используют, когда нужно обеспечить включение и отключение определенных приборов. Именно по этой схеме подсоединяются выключатели и тумблеры. Также схема хорошо подходит в тех случаях, когда необходимо сформировать электроцепь из потребителей с малым значением номинального напряжения.

При параллельном соединении конденсаторов совокупная емкость равняется сумме емкостей каждого полупроводника. В случае применения последовательного соединения конденсаторов, результирующая емкость уменьшается вдвое. Это свойство также используется при формировании электроцепей.

Способы соединения резисторов, решение задачи смешанного соединения проводников: видео

Источник: https://knigaelektrika.ru/teoriya/parallelnoe-i-posledovatelnoe-soedinenie-provodnikov-v-elektricheskoj-tsepi.html

Решение задач по электротехнике (ТОЭ)

Срок выполнения	от 1 дня
Цена	от 100 руб./задача
Предоплата	50 %
Кто будет выполнять?	преподаватель или аспирант

УЗНАТЬ СТОИМОСТЬ РАБОТЫТеоретические основы электротехники являются фундаментальной дисциплиной для всех электротехнических специальностей, а так же для некоторых неэлектротехнических (например, сварочное производство). На этой дисциплине основываются все спец. предметы электриков. Несмотря на большой объем дисциплины и кажущуюся сложность, она основана всего на нескольких законах. В этой статье я постараюсь рассмотреть решение основных задач, встречающихся в данном курсе.

Законы Кирхгофа. Расчет цепей постоянного тока

В электротехнике существует два основных закона, на основании которых, теоретически можно решить все цепи.
 

Первый закон Кирхгофа выглядит следующим образом.Сумма токов, входящих в узел, равна сумме токов, отходящих от узла.

Для данного рисунка имеем:I1 + I2 + I4 = I3 + I5.

Второй закон Кирхгофа.Сумма напряжений вдоль замкнутого контура равна сумме ЭДС вдоль этого же контура. Для схемы на рисунке (стрелкой обозначим направление вдоль контура, которое будем считать условно положительным).

Начиная с узла, где сходятся токи I1, I3, I4 запишем все напряжения (по закону Ома):-I1⋅R1 — I1⋅R2 – в первой ветви (знак минус означает, что ток имеет направление противоположное выбранному направлению контура).I3⋅R3 – во второй ветви (знак «плюс», направление совпадает).

Теперь запишем ЭДС:E2 — E3 (знак «минус» у E3, потому что направление ЭДС противоположно направлению контура).

Как видите, все довольно просто.
 

В большинстве случаев перед студентами стоит задача рассчитать величины токов во всех ветвях, зная величины ЭДС и резисторов. Для расчета сложной, разветвленной цепи постоянного тока, например этой, найденной на просторах интернета, воспользуемся следующими действиями.
 

 

Для начала задаемся условно положительными направлениями токов в ветвях (это значит, что ток может течь и в противоположном направлении, тогда он будет иметь отрицательное значение).
 

 

Составляем систему уравнений по второму закону Кирхгофа для каждого замкнутого контура так, чтобы охватить каждый неизвестный ток (в данной схеме имеем 3 таких контура). Направления контуров выбираем для удобства по часовой стрелке (хоть это и необязательно): 
 

Итого, имеем систему из 6 уравнений. Чтобы решить такую систему можно воспользоваться программой MathCad. Решается она следующим образом:
 

Это скриншот программы. Знак «равно» в уравнения должен быть жирным (вкладка «булевы», CTRL + “=/+”).MathCad может решать системы любого порядка (например, схема имеет 10 независимых контуров). Но, во-первых, функция “Given” не работает с комплексными числами (об этом позже), во-вторых, не всегда есть под рукой компьютер или условие задачи поставлено так, что требуется решить схему другим методом.

Данный метод решения задач называется методом непосредственного применения законов Кирхгофа. Большинство студентов старших курсов (уже прослушавших курс ТОЭ), инженеров-электриков, даже преподавателей и докторов наук могут решать схемы только этим методом, т.к. другие методы применяются крайне редко.
 

Переменный ток

Переменный синусоидальный ток (или напряжение) задается уравнением:

Здесь Im – амплитуда тока.ω – угловая частота, находится как ω = 2⋅π⋅f (обычно в условии задается либо f, либо ω)φ – фаза.

Обычно в задачах условия задают либо в таком формате, либо в действующем значении. Амплитудное больше действующего всегда в √2 раз. Если в условии задано просто значение (например, E1 = 220 В), то это значит, что дано действующее значение.
 

Если же в условии дано «250⋅sin(314t – 15°), В», то его нужно перевести в действующее комплексное значение.
 

Про комплексные числа можно подробнее прочитать на нашем сайте.
 

Для перевода величин к действующим необходимо: 

,

 

Точечка над I означает, что это комплекс.
 

Для заданного напряжения имеем: 
 

В решении задач обычно оперируют действующими значениями.
 

В переменном токе вводятся новые элементы:

Катушка индуктивности	L – [Гн]
Конденсатор [емкость]	С – [Ф]

Их сопротивления (реактивные сопротивления) находятся как:

(сопротивление конденсатора — отрицательное)

Например, имеем схему, она подключена на напряжение 200 В, имеющего частоту 100 Гц. Требуется найти ток. Параметры элементов заданы:
 

Чтоб найти ток, необходимо напряжение разделить на сопротивление (из закона Ома). Здесь основная задача – найти сопротивление. Комплексное сопротивление находится как:

 

Напряжение делим на сопротивление и получаем ток.
 

Все эти действия удобно проводить в MathCad. Комплексная единица ставится «1i» или «1j». Если нет возможности, то:

1. Деление удобно производить в показательной форме.
2. Сложение и вычитание – в алгебраической.
3. Умножение – в любой (оба числа в одинаковой форме).

Также, скажем пару слов о мощности. Мощность есть произведение тока и напряжения для цепей постоянного тока. Для цепей переменного тока вводится еще один параметр – угол сдвига фаз (вернее его косинус) между напряжением и током.
 

Предположим, для предыдущей цепи нашли ток и напряжение (в комплексной форме).

 

Также мощность можно найти и по другой формуле:

 

В этой формуле — сопряженный комплекс тока. Сопряженный – значит, что его мнимая часть (та, что с j) меняет свой знак на противоположный (минус/плюс).
Re – означает действительная часть (та, что без j).
 

Реактивная мощность цепи:

Im – мнимая часть комплексного числа (та, что с j).
 

Зная реактивную и активную мощность можно подсчитать полную мощность цепи:

 

Для упрощенного расчета цепей постоянного и переменного тока, содержащих большое число ветвей, пользуются одним из упрощенных методов анализа цепей. Рассмотрим подробнее метод контурных токов.
 

Метод контурных токов (МКТ)

Данный метод подходит для решения схем, содержащих больше узлов, чем независимых контуров (например, схема из раздела про постоянный ток). Принцип решения состоит в следующем:

1. Выделяем независимые контуры (их должно быть столько, чтоб охватить все неизвестные токи). Контурные токи обычно называют I11, I22 и т.д.

2. Определяем контурные сопротивления (сумма сопротивлений вдоль контура):

    

   Далее определяются общие контурные сопротивления (те, что относятся одновременно к 2 контурам), они берутся со знаком минус:

    

   Также определяем контурные ЭДС (алгебраическая сумма ЭДС вдоль контура):

3. Далее составляются уравнения (если имеем 4 контура, то система будет из 4 уравнений с 4 контурными токами в каждом, если из 5, то 5 и т.д.):

    

   Данная система легко решается методом Крамера. Также в сети есть много онлайн-калькуляторов.

4. Зная контурные токи, можно найти токи в ветвях:
   I1 = I11 (в первой ветви протекает только контурный ток I11)
   I2 = I33 – I22 (направления контурного тока I33 совпадает с направлением I2, направление I22 – противоположно, поэтому берем со знаком минус)
   По аналогии находим остальные токи.

Данный метод, как и другие (например, метод узловых потенциалов, эквивалентного генератора, наложения) пригоден для цепей как постоянного, так и переменного тока. При расчете цепей переменного тока сопротивления элементов приводятся к комплексной форме записи. Система уравнений решается также в комплексной форме.
 

Литература

Из литературы можно порекомендовать Бессонова Л.А. «Теоретические основы электротехники: Электрические цепи». Также много информации в интернете на сайтах, посвященных электротехнике. 

Решение электротехники на заказ

И помните, что наши решатели всегда готовы помочь Вам с ТОЭ. Подробнее.

Источник: https://Reshatel.org/reshenie-zadach/reshenie-zadach-po-toe/

10 формул

Доброго дня уважаемые радиолюбители!
Приветствую вас на сайте “Радиолюбитель“

Формулы составляют скелет науки об электронике. Вместо того, чтобы сваливать на стол целую кучу радиоэлементов, а потом переподключать их между собой, пытаясь выяснить, что же появится на свет в результате, опытные специалисты сразу строят новые схемы на основе известных математических и физических законов. Именно формулы помогают определять конкретные значения номиналов электронных компонентов и рабочих параметров схем.

Точно так же эффективно использовать формулы для модернизации уже готовых схем. К примеру, для того, чтобы выбрать правильный резистор в схеме с лампочкой, можно применить базовый закон Ома для постоянного тока (о нем можно будет прочесть в разделе “Соотношения закона Ома” сразу после нашего лирического вступления). Лампочку можно заставить, таким образом, светить более ярко или, наоборот — притушить.

В этой главе будут приведены многие основные формулы физики, с которыми рано или поздно приходится сталкиваться в процессе работы в электронике. Некоторые из них известны уже столетия, но мы до сих пор продолжаем ими успешно пользоваться, как будут пользоваться и наши внуки.

Соотношения закона Ома

Закон Ома представляет собой взаимное соотношение между напряжением, током, сопротивлением и мощностью. Все выводимые формулы для расчета каждой из указанных величин представлены в таблице:

Искомая величина	Формула
Напряжение, В	U=I*R
Ток, А	I=U/R
Сопротивление, Ом	R=U/I
Мощность, Вт	P=U*I

В этой таблице используются следующие общепринятые обозначения физических величин:

U — напряжение (В),

I — ток (А),

Р — мощность (Вт),

R — сопротивление (Ом),

Потренируемся на следующем примере: пусть нужно найти мощность схемы. Известно, что напряжение на ее выводах составляет 100 В, а ток— 10 А. Тогда мощность согласно закону Ома будет равна 100 х 10 = 1000 Вт. Полученное значение можно использовать для расчета, скажем, номинала предохранителя, который нужно ввести в устройство, или, к примеру, для оценки счета за электричество, который вам лично принесет электрик из ЖЭК в конце месяца.

А вот другой пример: пусть нужно узнать номинал резистора в цепи с лампочкой, если известно, какой ток мы хотим пропускать через эту цепь. По закону Ома ток равен:

I = U / R

Схема, состоящая из лампочки, резистора и источника питания (батареи) показана на рисунке. Используя приведенную формулу, вычислить искомое сопротивление сможет даже школьник.

Что же в этой формуле есть что? Рассмотрим переменные подробнее.

>U пит (иногда также обозначается как V или Е): напряжение питания. Вследствие того, что при прохождении тока через лампочку на ней падает какое-то напряжение, величину этого падения (обычно рабочее напряжение лампочки, в нашем случае 3,5 В) нужно вычесть из напряжения источника питания. К примеру, если Uпит = 12 В, то U = 8,5 В при условии, что на лампочке падает 3,5 В.

>  I: ток (измеряется в амперах), который планируется пропустить через лампочку. В нашем случае – 50 мА. Так как в формуле ток указывается в амперах, то 50 миллиампер составляет лишь малую его часть: 0,050 А.

>R: искомое сопротивление токоограничивающего резистора, в омах.

В продолжение, можно проставить в формулу расчета сопротивления реальные цифры вместо U, I и R:

R = U/I = 8,5 В / 0,050 А= 170 Ом

Расчёты сопротивления

Рассчитать сопротивление одного резистора в простой цепи достаточно просто. Однако с добавлением в нее других резисторов, параллельно или последовательно, общее сопротивление цепи также изменяется. Суммарное сопротивление нескольких соединенных последовательно резисторов равно сумме отдельных сопротивлений каждого из них. Для параллельного же соединения все немного сложнее.

Почему нужно обращать внимание на способ соединения компонентов между собой? На то есть сразу несколько причин.

> Сопротивления резисторов составляют только некоторый фиксированный ряд номиналов. В некоторых схемах значение сопротивления должно быть рассчитано точно, но, поскольку резистор именно такого номинала может и не существовать вообще, то приходится соединять несколько элементов последовательно или параллельно.

> Резисторы — не единственные компоненты, которые имеют сопротивление. К примеру, витки обмотки электромотора также обладают некоторым сопротивлением току. Во многих практических задачах приходится рассчитывать суммарное сопротивление всей цепи.

Расчет сопротивления последовательных резисторов

Формула для вычисления суммарного сопротивления резисторов, соединенных между собой последовательно, проста до неприличия. Нужно просто сложить все сопротивления:

Rобщ = Rl + R2 + R3 + … (столько раз, сколько есть элементов)

В данном случае величины Rl, R2, R3 и так далее — сопротивления отдельных резисторов или других компонентов цепи, а Rобщ — результирующая величина.

Так, к примеру, если имеется цепь из двух соединенных последовательно резисторов с номиналами 1,2 и 2,2 кОм, то суммарное сопротивление этого участка схемы будет равно 3,4 кОм.

Расчет сопротивления параллельных резисторов

Все немного усложняется, если требуется вычислить сопротивление цепи, состоящей из параллельных резисторов. Формула приобретает вид:

R общ = R1 * R2 / (R1 ­­+ R2)

где R1 и R2 — сопротивления отдельных резисторов или других элементов цепи, а Rобщ -результирующая величина. Так, если взять те же самые резисторы с номиналами 1,2 и 2,2 кОм, но соединенные параллельно, получим

776,47 = 2640000 / 3400

Для расчета результирующего сопротивления электрической цепи из трех и более резисторов используется следующая формула:

Здесь снова величины Rl, R2, R3 и так далее — сопротивления отдельных резисторов, a Rобщ — суммарная величина.

Расчёты ёмкости

Формулы, приведенные выше, справедливы и для расчета емкостей, только с точностью до наоборот. Так же, как и для резисторов, их можно расширить для любого количества компонентов в цепи.

Расчет емкости параллельных конденсаторов

Если нужно вычислить емкость цепи, состоящей из параллельных конденсаторов, необходимо просто сложить их номиналы:

Собщ = CI + С2 + СЗ + …

В этой формуле CI, С2 и СЗ — емкости отдельных конденсаторов, а Собщ суммирующая величина.

Расчет емкости последовательных конденсаторов

Для вычисления общей емкости пары связанных последовательно конденсаторов применяется следующая формула:

Собщ  = С1 * С2 /( С1+С2)

где С1 и С2 — значения емкости каждого из конденсаторов, а Собщ — общая емкость цепи

Расчет емкости трех и более последовательно соединенных конденсаторов

В схеме имеются конденсаторы? Много? Ничего страшного: даже если все они связаны последовательно, всегда можно найти результирующую емкость этой цепи:

И здесь опять величины C1, С2, СЗ и так далее — емкости отдельных конденсаторов, а Собщ. — суммарная величина.

https://www.youtube.com/watch?v=OP6nJnzO1Sc

Так зачем же вязать последовательно сразу несколько конденсаторов, когда могло хватить одного? Одним из логических объяснений этому факту служит необходимость получения конкретного номинала емкости цепи, аналога которому в стандартном ряду номиналов не существует. Иногда приходится идти и по более тернистому пути, особенно в чувствительных схемах, как, например, радиоприемники.

Расчёт энергетических уравнений

Наиболее широко на практике применяют такую единицу измерения энергии, как киловатт-часы или, если это касается электроники, ватт-часы. Рассчитать затраченную схемой энергию можно, зная длительность времени, на протяжении которого устройство включено. Формула для расчета такова:

ватт-часы = Р х Т

В этой формуле литера Р обозначает мощность потребления, выраженную в ваттах, а Т — время работы в часах. В физике принято выражать количество затраченной энергии в ватт-секундах, или Джоулях. Для расчета энергии в этих единицах ватт-часы делят на 3600.

Расчёт постоянной ёмкости RC-цепочки

В электронных схемах часто используются RC-цепочки для обеспечения временных задержек или удлинения импульсных сигналов. Самые простые цепочки состоят всего лишь из резистора и конденсатора (отсюда и происхождение термина RC-цепочка).

Принцип работы RC-цепочки состоит в том, что заряженный конденсатор разряжается через резистор не мгновенно, а на протяжении некоторого интервала времени. Чем больше сопротивление резистора и/или конденсатора, тем дольше будет разряжаться емкость. Разработчики схем очень часто применяют RC-цепочки для создания простых таймеров и осцилляторов или изменения формы сигналов.

Каким же образом можно рассчитать постоянную времени RC-цепочки? Поскольку эта схема состоит из резистора и конденсатора, в уравнении используются значения сопротивления и емкости. Типичные конденсаторы имеют емкость порядка микрофарад и даже меньше, а системными единицами являются фарады, поэтому формула оперирует дробными числами.

T = RC

Пусть, к примеру, имеется резистор 2000 Ом, подключенный к конденсатору 0,1 мкФ. Постоянная времени этой цепочки будет равна 0,002 с, или 2 мс.

Для того чтобы на первых порах облегчить вам перевод сверхмалых единиц емкостей в фарады, мы составили таблицу:

Значение емкости конденсатора, мкФ	Емкость конденсатора для расчета
10	0,000 01
1	0,000 001
0,1	0,000 000 1
0,01	0,000 000 01

Расчёты частоты и длины волны

Частота сигнала является величиной, обратно пропорциональной его длине волны, как будет видно из формул чуть ниже. Эти формулы особенно полезны при работе с радиоэлектроникой, к примеру, для оценки длины куска провода, который планируется использовать в качестве антенны. Во всех следующих формулах длина волны выражается в метрах, а частота — в килогерцах.

Расчет частоты сигнала

Предположим, вы хотите изучать электронику для того, чтобы, собрав свой собственный приемопередатчик, поболтать с такими же энтузиастами из другой части света по аматорской радиосети. Частоты радиоволн и их длина стоят в формулах бок о бок. В радиолюбительских сетях часто можно услышать высказывания о том, что оператор работает на такой-то и такой длине волны. Вот как рассчитать частоту радиосигнала, зная длину волны:

Частота = 300000 / длина волны

Длина волны в данной формуле выражается в миллиметрах, а не в футах, аршинах или попугаях. Частота же дана в мегагерцах.

Расчет длины волны сигнала

Ту же самую формулу можно использовать и для вычисления длины волны радиосигнала, если известна его частота:

Длина волны = 300000 / Частота

Результат будет выражен в миллиметрах, а частота сигнала указывается в мегагерцах.

Приведем пример расчета. Пусть радиолюбитель общается со своим другом на частоте 50 МГц (50 миллионов периодов в секунду). Подставив эти цифры в приведенную выше формулу, получим:

6000 миллиметров = 300000 / 50 МГц

Однако чаще пользуются системными единицами длины — метрами, поэтому для завершения расчета нам остается перевести длину волны в более понятную величину. Так как в 1 метре 1000 миллиметров, то в результате получим 6 м. Оказывается, радиолюбитель настроил свою радиостанцию на длину волны 6 метров. Прикольно!

Источник: http://radio-stv.ru/nachinayushhim-radiolyubitelyam/10-formul

Параллельное соединение резисторов. Калькулятор для расчета

Параллельное соединение резисторов — одно из двух видов электрических соединений, когда оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов. Зачастую резисторы соединяют последовательно или параллельно для того, чтобы создать более сложные электронные схемы.

Схема параллельного соединения резисторов показан на рисунке ниже. При параллельном соединении резисторов, напряжение на всех резисторах будет одинаковым, а протекающий через них ток будет пропорционален их сопротивлению:

Формула параллельного соединения резисторов

Общее сопротивление нескольких резисторов соединенных параллельно определяется по следующей формуле:

Ток, протекающий через отдельно взятый резистор, согласно закону Ома, можно найти по формуле:

При разработке устройства, возникла необходимость установить резистор с сопротивлением 8 Ом. Если мы просмотрим весь номинальный ряд стандартных значений резисторов, то мы увидим, что резистора с сопротивлением в 8 Ом в нем нет.

Данное уравнение показывает, что если R1 равен R2, то сопротивление R составляет половину сопротивления одного из двух резисторов. При R = 8 Ом, R1 и R2 должны, следовательно, иметь значение 2 × 8 = 16 Ом.
Теперь проведем проверку, рассчитав общее сопротивление двух резисторов:

Таким образом, мы получили необходимое сопротивление 8 Ом, соединив параллельно два резистора по 16 Ом.

Пример расчета №2

Найти общее сопротивление  R из трех параллельно соединенных резисторов:

Общее сопротивление R рассчитывается по формуле:

Этот метод расчета может быть использованы для расчета любого количества отдельных сопротивлений соединенных параллельно.

Один важный момент, который необходимо запомнить при расчете параллельно соединенных резисторов – это то, что общее сопротивление всегда будет меньше, чем значение наименьшего сопротивления в этой комбинации.

Как рассчитать сложные схемы соединения резисторов

Более сложные соединения резисторов могут быть рассчитаны путем систематической группировки резисторов. На рисунке ниже необходимо посчитать общее сопротивление цепи, состоящей из трех резисторов:

Для простоты расчета, сначала сгруппируем резисторы по параллельному и последовательному типу соединения.

Резисторы R2 и R3 соединены последовательно (группа 2). Они в свою очередь соединены параллельно с резистором R1 (группа 1).

Последовательное соединение резисторов группы 2 вычисляется как сумма сопротивлений R2 и R3:

Расчет более сложных соединений резисторов можно выполнить используя законы Кирхгофа.

Ток, протекающий в цепи параллельно соединенных резисторах

Общий ток I протекающий в цепи параллельных резисторов равняется сумме отдельных токов, протекающих во всех параллельных ветвях, причем ток в отдельно взятой ветви не обязательно должен быть равен току в соседних ветвях.

Несмотря на параллельное соединение, к каждому резистору приложено одно и то же напряжение. А поскольку величина сопротивлений в параллельной цепи может быть разной, то и величина протекающего тока через каждый резистор тоже будет отличаться (по определению закона Ома).

Рассмотрим это на примере двух параллельно соединенных резисторов. Ток, который течет через каждый из резисторов ( I1 и I2 ) будет отличаться друг от друга поскольку сопротивления резисторов R1 и R2 не равны.
Однако мы знаем, что ток, который поступает в цепь в точке «А» должен выйти из цепи в точке «B» .

Первое правило Кирхгофа гласит: «Общий ток, выходящий из цепи равен току входящий в цепь».

Таким образом, протекающий общий ток в цепи  можно определить как:

I = I1 + I2

Затем с помощью закона Ома можно вычислить ток, который протекает через каждый резистор:

Ток, протекающий в R1 = U ÷ R1 = 12 ÷ 22 кОм = 0,545 мА

Ток, протекающий в R 2 = U ÷ R2 = 12 ÷ 47 кОм = 0,255 мА

Таким образом, общий ток будет равен:

I = 0,545 мА + 0,255 мА = 0,8 мА

Это также можно проверить, используя закон Ома:

I = U ÷ R = 12 В ÷ 15 кОм = 0,8 мА (то же самое)

где 15кОм — это общее сопротивление двух параллельно соединенных резисторов (22 кОм и 47 кОм)

И в завершении хочется отметить, что большинство современных резисторов маркируются цветными полосками и назначение ее можно узнать здесь.

Параллельное соединение резисторов — онлайн калькулятор

Чтобы быстро вычислить общее сопротивление двух и более резисторов, соединенных параллельно, вы можете воспользоваться следующим онлайн калькулятором:

Подведем итог

Когда два или более резистора соединены так, что оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов, то говорят, что они соединены между собой параллельно. Напряжение на каждом резисторе внутри параллельной комбинации одинаковое, но токи, протекающие через них, могут отличаться друг от друга, в зависимости от величины сопротивлений каждого резистора.

Эквивалентное или полное сопротивление параллельной комбинации всегда будет меньше минимального сопротивления резистора, входящего в параллельное соединение.

Источник: http://www.joyta.ru/7362-parallelnoe-soedinenie-rezistorov/

Последовательное и параллельное соединение проводников

Цели урока:

Образовательные:

• познакомить учащихся с последовательным и параллельным соединениями проводников;
• познакомить учащихся с закономерностями, существующими в цепи с последовательным и параллельным соединениями проводников;

Развивающие:

• развивать способности учащихся анализировать, сравнивать, делать выводы.
• развивать умение решать задачи.

Воспитательные:

• воспитывать самореализацию у учащихся, взаимопонимание и уверенность в знаниях

Наглядные пособия и оборудование:

• презентация (приложение);
• мультимедийный проектор;
• цепи с последовательно и параллельно соединёнными лампочками.

План урока:

• Вводная часть. – Сообщение учителя.
• Актуализация знаний. – Фронтальный опрос.
• Последовательное и параллельное соединение проводников. – Демонстрация, беседа, презентация,  объяснение нового материала, работа с таблицей.
• Физкультминутка.
• Закрепление изученного материала. – Работа с презентацией. Решение задач.
• Подведение итогов, домашнее задание. – Сообщение учителя.

Актуализация знаний

Вопросы для учащихся находятся на слайдах презентации:

• Что называется сопротивлением?
• В чём причина сопротивления?
• От каких параметров зависит сопротивление проводника?
• Сформулируйте закон Ома для участка цепи.
• Силу тока в цепи увеличили в два раза. Как изменилось сопротивление проводника?
• Напряжение в цепи уменьшили в два раза. Как изменилось сопротивление проводника?
• Длину проводника уменьшили в три раза. Как изменилось сопротивление проводника?
• Проволоку согнули пополам. Как изменилось сопротивление проволоки?

Последовательное и параллельное соединения проводников:

На слайде появляется таблица, учащиеся переносят её в тетрадь.

Последовательное соединение	Параллельное соединение
Схема
Сила тока
Напряжение
Сопротивление

Обсуждается последовательное соединение проводников.

Последовательное соединение – соединение, при котором конец первого проводника соединяют с началом второго, конец второго – с началом третьего и т.д.

Учитель демонстрирует опыты с цепью с последовательно соединёнными лампочками.

Учащиеся делают выводы:

• сила тока в цепи при последовательном соединении проводников в любых частях цепи одинакова: I = I1 = I2
• общее напряжение в цепи равно сумме напряжений на каждом участке: U = U1 + U2

Обсуждается вопрос: Чему рано общее сопротивление цепи при последовательном соединении проводников?

С помощью закономерностей и закона Ома для участка цепи выводится формула для общего сопротивления проводников: R = R1 + R2.

Обсуждается вопрос: Как найти сопротивление n последовательно соединённых одинаковых проводников? R = nR1

Обсуждается параллельное соединение проводников.

Параллельное соединение – соединение, при котором начала всех проводников присоединяются к одной точке цепи, а их концы к другой.

Учитель демонстрирует опыты с цепью с параллельно соединёнными лампочками.

Учащиеся делают выводы:

• cила тока в неразветвлённой цепи равна сумме токов в разветвлениях: I = I1 + I2
• yапряжение на каждом из параллельно соединённых проводников одинаково: U = U1 = U2

Обсуждается вопрос: Чему рано общее сопротивление цепи при параллельном соединении проводников?

С помощью закономерностей и закона Ома для участка цепи выводится формула для общего сопротивления проводников:

Обсуждается вопрос: Как найти сопротивление n параллельно соединённых одинаковых проводников?

Преимущества и недостатки соединений.

Пример последовательного соединения: гирлянда.

Пример параллельного соединения: потребители в жилых помещениях.

Преимущества и недостатки соединений:

Последовательное – защита цепей от перегрузок: при увеличении силы тока выходит из строя предохранитель, и цепь автоматически отключается. При выходе из строя одного из элементов соединения отключаются и остальные.

Параллельное– при выходе из строя одного из элементов соединения, остальные действуют. При включении элемента с меньшим возможным напряжением в цепь элемент перегорит.

Закрепление изученного материала

Решение задач на последовательное и параллельное соединения с использованием слайдов презентации .№ 1382,1386 из «Сборника задач по физике 7-9» В.И. Лукашик и др.

Домашнее задание: § 48,49, упр. 22 (1), 23 (1).

Рефлексия

Проведите стрелочки к тем утверждениям, которые соответствуют вашему состоянию в конце урока.

Источник: https://rosuchebnik.ru/material/posledovatelnoe-i-parallelnoe-soedinenie-provodnikov-7825/

Последовательное и параллельное соединения проводников – FIZI4KA

ОГЭ 2018 по физике ›

1. Потребители электрической энергии: электрические лампочки, резисторы и пр. — могут по-разному соединяться друг с другом в электрической цепи. Существует два основных типа соединения проводников: последовательное и параллельное. При последовательном соединении проводников конец одного проводника соединяется с началом другого проводника, а его конец — с началом третьего и т.д. (рис. 85).

Примером последовательного соединения проводников может служить соединение электрических лампочек в ёлочной гирлянде.

При последовательном соединении проводников ток проходит через все лампочки, при этом через поперечное сечение каждого проводника в единицу времени проходит одинаковый заряд, т.е. заряд не скапливается ни в какой части проводника. Поэтому при последовательном соединении проводников сила тока в любом участке цепи одинакова: ​\( I_1=I_2=I \)​.

Общее сопротивление последовательно соединённых проводников равно сумме их сопротивлений: ​\( R_1=R_2=R \)​. Это следует из того, что при последовательном соединении проводников их общая длина увеличивается, она больше, чем длина каждого отдельного проводника, соответственно увеличивается и сопротивление проводников.

По закону Ома напряжение на каждом проводнике равно: ​\( U_1=IR_1 \)​, ​\( U_2=IR_2 \)​, а общее напряжение равно ​\( U=I(R_1+R_2) \)​. Поскольку сила тока во всех проводниках одинакова, а общее сопротивление равно сумме сопротивлений проводников, то полное напряжение на последовательно соединённых проводниках равно сумме напряжений на каждом проводнике: ​\( U=U_1+U_2 \)​.

Из приведённых равенств следует, что последовательное соединение проводников используется в том случае, если напряжение, на которое рассчитаны потребители электрической энергии, меньше общего напряжения в цепи.

2. Примером параллельного соединения проводников служит соединение потребителей электрической энергии в квартире. Так, электрические лампочки, чайник, утюг и пр. включаются параллельно.

При параллельном соединении проводников все проводники одним своим концом присоединяются к одной точке цепи (А), а вторым концом к другой точке цепи (В) (рис. 86).

Поэтому вольтметр, подключенный к этим точкам, покажет напряжение как на проводнике 1, так и на проводнике 2. Таким образом, напряжение на концах всех параллельно соединённых проводников одно и то же: ​\( U_1=U_2=U \)​.

При параллельном соединении проводников электрическая цепь разветвляется, в данном случае в точке В. Поэтому часть общего заряда проходит через один проводник, а часть — через другой. Следовательно при параллельном соединении проводников сила тока в неразветвлённой части цепи равна сумме силы тока в отдельных проводниках: ​\( I=I_1+I_2 \)​.

В соответствии с законом Ома ​\( I=\frac{U}{R} \)​, \( I_1=\frac{U_1}{R_1} \), \( I_2=\frac{U_2}{R_2} \). Отсюда следует: ​\( \frac{U}{R}=\frac{U_1}{R_1}+\frac{U_2}{R_2} \)​. Так как ​\( U_1=U_2=U \)​, \( \frac{1}{R}=\frac{1}{R_1}+\frac{1}{R_2} \). Величина, обратная общему сопротивлению параллельно соединенных проводников, равна сумме величин, обратных сопротивлению каждого проводника.

При параллельном соединении проводников их общее сопротивление меньше, чем сопротивление каждого проводника. Действительно, если параллельно соединены два проводника, имеющие одинаковое сопротивление ​\( r \)​, то их общее сопротивление равно: ​\( R=r/2 \)​. Это объясняется тем, что при параллельном соединении проводников как бы увеличивается площадь их поперечного сечения, соответственно уменьшается сопротивление.

Из приведённых формул понятно, почему потребители электрической энергии включаются параллельно: они все рассчитаны на определённое одинаковое напряжение, которое в квартирах равно 220 В. Зная сопротивление каждого потребителя, можно рассчитать силу тока в каждом из них и соответствие суммарной силы тока предельно допустимой силе тока.

• Примеры заданий
• Ответы

Часть 1

1. На рисунке изображёна схема участка электрической цепи АВ. В эту цепь параллельно включены два резистора сопротивлением ​\( R_1 \)​ и ​\( R_2 \)​. Напряжения на резисторах соответственно ​\( U_1 \)​ и ​\( U_2 \)​.

По какой из формул можно определить напряжение U на участке АВ?

1) ​\( U=U_1+U_2 \)​
2) ​\( U=U_1-U_2 \)​
3) ​\( U=U_1=U_2 \)​
4) ​\( U=\frac{U_1U_2}{U_1+U_2} \)​

2. На рисунке изображёна схема электрической цепи, содержащая два параллельно включённых резистора сопротивлением ​\( R_1 \)​ и ​\( R_2 \)​. Какое из приведённых ниже соотношений справедливо для такого соединения резисторов?

1) ​\( I=I_1=I_2 \)​
2) \( I=I_1+I_2 \)
3) \( U=U_1+U_2 \)
4) \( R=R_1+R_2 \)

3. На рисунке изображена схема электрической цепи. В эту цепь последовательно включены два резистора сопротивлением R} и R2. Какое из приведённых ниже соотношений справедливо для такого соединения резисторов?

1) ​\( U=U_1+U_2 \)​
2) \( I=I_1+I_2 \)
3) \( U=U_1=U_2 \)
4) \( R=\frac{R_1R_2}{R_1+R_2} \)

4. На рисунке изображена схема электрической цепи. В эту цепь последовательно включены два резистора сопротивлением ​\( R_1 \)​ и ​\( R_2 \)​. Какое из приведённых ниже соотношений справедливо для такого соединения резисторов?

5. На рисунке изображена схема электрической цепи. В эту цепь параллельно включены два одинаковых резистора сопротивлением ​\( R_1 \)​. По какой из формул можно определить общее сопротивление цепи ​\( R \)​?

1) ​\( R=R_1{}2 \)​
2) ​\( R=2R_1 \)​
3) ​\( R=\frac{R_1}{2} \)​
4) ​\( R=\sqrt{R_1} \)​

6. Общее сопротивление участка цепи, изображённого на рисунке, равно 9 Ом. Сопротивления резисторов ​\( R_1 \)​ и ​\( R_2 \)​ равны. Чему равно сопротивление каждого резистора?

1) 81 Ом 2) 18 Ом 3) 9 Ом

4) 4,5 Ом

7. Чему равно сопротивление участка цепи, содержащего три последовательно соединенных резистора сопротивлением по 9 Ом каждый?

1) 1/3 Ом 2) 3 Ом 3) 9 Ом

4) 27 Ом

8. Чему равно общее сопротивление участка цепи, изображённого на рисунке, если ​\( R_1 \)​ = 1 Ом, ​\( R_2 \)​ = 10 Ом, ​\( R_3 \)​ = 10 Ом, ​\( R_4 \)​ = 5 Ом?

1) 9 Ом 2) 11 Ом 3) 16 Ом

4) 26 Ом

9. Чему равно общее сопротивление участка цепи, изображённого на рисунке, если \( R_1 \) = 1 Ом, \( R_2 \) = 3 Ом, \( R_3 \) = 10 Ом, \( R_4 \) = 10 Ом?

1) 9 Ом 2) 10 Ом 3) 14 Ом

4) 24 Ом

10. Если ползунок реостата (см. схему) переместить влево, то сила тока

1) в резисторе ​\( R_1 \)​ уменьшится, а в резисторе ​\( R_2 \)​ увеличится 2) увеличится в обоих резисторах

3) в резисторе ​\( R_1 \)​ увеличится, а в резисторе ​\( R_2 \)​ уменьшится

4) уменьшится в обоих резисторах

11. На рисунке изображена электрическая цепь, состоящая из источника тока, резистора и реостата. Как изменяются при передвижении ползунка реостата вправо его сопротивление, сила тока в цепи и напряжение на резисторе 1?

Для каждой физической величины определите соответствующий характер изменения. Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

ФИЗИЧЕСКАЯ ВЕЛИЧИНА A) сопротивление реостата 2 Б) сила тока в цепи

B) напряжение на резисторе 1

ХАРАКТЕР ИЗМЕНЕНИЯ 1) увеличивается 2) уменьшается

3) не изменяется

12. Установите соответствие между физическими величинами и правильной электрической схемой для измерения этих величин при последовательном соединении двух резисторов ​\( R_1 \)​ и \( R_2 \). Запишите в таблицу выбранные цифры под соответствующими буквами. Цифры в ответе могут повторяться.

ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ
A) сила тока в резисторе \( R_1 \)​ и \( R_2 \)
Б) напряжение на резисторе \( R_2 \)
B) общее напряжение на резисторах \( R_1 \)​ и \( R_2 \)

Часть 2

13. Три резистора соединены, как показано на рисунке. Сопротивления резисторов ​\( R_1 \)​ = 10 Ом, \( R_2 \) = 5 Ом, \( R_3 \) = 5 Ом. Каково напряжение на резисторе 1, если амперметр показывает силу тока 2 А?

Ответы

Источник: https://fizi4ka.ru/ogje-2018-po-fizike/posledovatelnoe-i-parallelnoe-soedinenija-provodnikov.html