Расчет цепей постоянного тока — студопедия
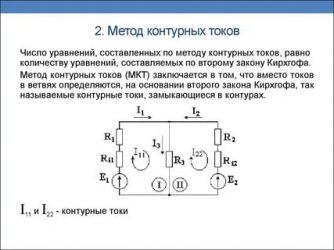
В цепи постоянного тока действуют постоянные напряжения, протекают постоянные токи и присутствуют только резистивные элементы (сопротивления).
Идеальным источником напряжения называют источник, напряжение на зажимах которого, создаваемое внутренней электродвижущей силой (ЭДС ), на зависит от формируемого им в нагрузке тока (рис. 6.1а). При этом имеет место равенство . Вольтамперная характеристика идеального источника напряжения показана на рис. 6.1б.
Рис. 6.1
Идеальным источником тока называют источник, который отдает в нагрузку ток, не зависящий от напряжения на зажимах источника, Рис. 6.2а. Его вольтамперная характеристика показана на рис. 6.2б.
Рис. 6.2
В сопротивлении связь между напряжением и током определяется законом Ома в виде
. (6.1)
Пример электрической цепи показан на рис. 6.3. В ней выделяются ветви, состоящие из последовательного соединения нескольких элементов (источника E и сопротивления ) или одного элемента ( и ) и узлы – точки соединения трех и более ветвей, отмеченные жирными точками. В рассмотренном примере имеется ветви и узла.
Рис. 6.3
Кроме того, в цепи выделяются независимые замкнутые контуры, не содержащие идеальные источники тока. Их число равно . В примере на рис. 6.3 их число , например, контуры с ветвями E и , показанные на рис. 6.3 овалами со стрелками, указывающими положительное направление обхода контура.
Связь токов и напряжений в цепи определяется законами Кирхгофа.
Первый закон Кирхгофа: алгебраическая сумма токов, сходящихся в узле электрической цепи, равна нулю,
. (6.2)
Втекающие в узел токи имеют знак плюс, а вытекающие минус.
Второй закон Кирхгофа: алгебраическая сумма напряжений на элементах замкнутого независимого контура равна алгебраической сумме ЭДС идеальных источников напряжения, включенных в этом контуре,
. (6.3)
Напряжения и ЭДС берутся со знаком плюс, если их положительные направления совпадают с направлением обхода контура, в противном случае используется знак минус.
Для приведенного на рис. 6.3 примера по закону Ома получим подсистему компонентных уравнений
(6.4)
По законам Кирхгофа подсистема топологических уравнений цепи имеет вид
(6.5)
Расчет на основе закона Ома
Этот метод удобен для расчета сравнительно простых цепей с одним источником сигнала. Он предполагает вычисление сопротивлений участков цепи, для которых известна вели-
чина тока (или напряжения), с последующим определением неизвестного напряжения (или тока). Рассмотрим пример расчета цепи, схема которой приведена на рис. 6.4, при токе идеального источника А и сопротивлениях Ом, Ом, Ом. Необходимо определить токи ветвей и , а также напряжения на сопротивлениях , и .
Известен ток источника , тогда можно вычислить сопротивление цепи относительно зажимов источника тока (параллельного соединения сопротивления и последовательно соединен-
Рис. 6.4 ных сопротивлений и ),
.
Напряжение на источнике тока (на сопротивлении ) равно
В.
Затем можно найти токи ветвей
А,
А.
Полученные результаты можно проверить с помощью первого закона Кирхгофа в виде . Подставляя вычисленные значения, получим А, что совпадает с величиной тока источника.
Зная токи ветвей, нетрудно найти напряжения на сопротивлениях (величина уже найдена)
В,
В.
По второму закону Кирхгофа . Складывая полученные результаты, убеждаемся в его выполнении.
Расчет цепи по уравнениям Кирхгофа
Проведем расчет токов и напряжений в цепи, показанной на рис. 6.3 при и . Цепь описывается системой уравнений (6.4) и (6.5), из которой для токов ветвей получим
(6.6)
Из первого уравнения выразим , а из третьего
.
Тогда из второго уравнения получим
,
и, следовательно
,
.
Из уравнений закона Ома запишем
.
.
Нетрудно убедиться, что выполняется второй закон Кирхгофа
.
Подставляя численные значения, получим
, ,
, .
https://www.youtube.com/watch?v=bR_cJDOMjxo
Эти же результаты можно получить, используя только закон Ома.
Мощность в цепи постоянного тока
Действующие в цепи идеальные источники тока и (или) напряжения отдают мощность в подключенную к ним цепь (нагрузку). Для цепи на рис. 6.1а отдаваемая идеальным источником напряжения мощность равна
, (6.7)
а в цепи на рис. 6.2а идеальный источник тока отдает в нагрузку мощность
. (6.8)
Подключенная к источнику внешняя резистивная цепь потребляет от него мощность, преобразуя ее в другте виды энергии, чаще всего в тепло.
Если через сопротивление протекает ток , а приложенное к нему напряжение равно , то для потребляемой сопротивлением мощности получим
. (6.9)
С учетом уравнений закона Ома (6.1) можно записать
. (6.10)
Если в цепи несколько сопротивлений, то сумма потребляемых ими мощностей равна суммарной мощности, отдаваемой в цепь всеми действующими в ней источниками. Это условие баланса мощностей.
Например, для цепи на рис. 6.3 в общем виде получим
. (6.11)
Подставляя в левую часть равенства (6.11) полученные ранее выражения для токов, получим
что соответствует правой части выражения (6.11).
Аналогичные расчеты можно проделать и для цепи на рис. 6.4.
Условие баланса мощностей позволяет дополнительно контролировать правильность расчетов.
Источник: https://studopedia.ru/7_42126_raschet-tsepey-postoyannogo-toka.html
Расчет электрических цепей
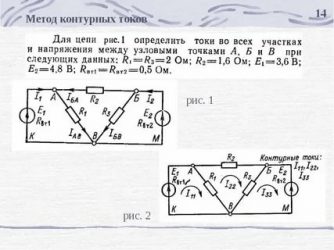
> Теория > Расчет электрических цепей
На практике разработан ряд методов для определения и расчета схем с постоянным током, что предоставляет возможность уменьшить трудоемкий процесс вычисления трудных электрических цепей. Основными законами, с помощью которых определяются характеристики практически каждой схемы, являются постулаты Кирхгофа.
Пример сложных электрических цепей
Пути вычисления электрических схем
Расчет электрических цепей разветвляется на множество методов, используемых на практике, а именно: метод эквивалентных преобразований, прием, основанный на постулатах Ома и Кирхгофа, способ наложения, способ контурных токов, метод узловых потенциалов, метод идентичного генератора.
Процесс расчета электрической цепи состоит из нескольких обязательных этапов, позволяющих довольно быстро и точно произвести все расчеты.
Перед тем, как узнать или вычислить необходимые параметры, рассчитываемая электрическая цепь переносится схематически на бумагу, где содержатся символические обозначения входящих в ее состав элементов и порядок их соединения.
Все элементы и устройства подразделяются на три категории:
- Источники электропитания. Основным признаком данного элемента является превращение неэлектрической энергии в электрическую. Эти источники энергии именуются первичными источниками энергии. Вторичные источники энергии представляют собой такие устройства, на входах и выходах которых присутствует электрическая энергия. К ним относятся выпрямительные приборы или трансформаторы напряжения;
- Устройства, потребляющие электрическую энергию. Такие элементы преобразовывают электрическую энергию в любую другую, будь то свет, звук, тепло и тому подобные виды;
- Вспомогательные элементы цепи, к которым относятся провода соединений, аппаратура коммутации, защиты и другие подобные элементы.
Также к основным понятиям электрической схемы относятся:
- Ветвь электрической схемы – участок цепи с одним и тем же током. В состав такой ветви могут входить один или несколько последовательно соединенных элементов;
- Узел электрической схемы – точка соединения трех и более ветвей схемы;
- Контур электрической схемы, представляющий собой любой замкнутый путь, проходящий по нескольким ветвям.
Обозначение ветвей, узлов и контуров на схеме
Метод расчета по законам Ома и Кирхгофа
Расчет емкости конденсатора
Данные законы позволяют узнать силу тока и найти взаимосвязь между значениями токов, напряжений, ЭДС всей цепи и единичных участков.
Закон Ома для участка цепи
По закону Ома соотношение тока, напряжения и сопротивления цепи выглядит как:
UR=RI.
Исходя из этой формулы, найти силу тока можно по выражению:
I=UR/R, где:
- UR – напряжение или падение напряжения на резисторе;
- I – ток в резисторе.
Закон Ома для полной цепи
В законе Ома для полной цепи дополнительно используется величина внутреннего сопротивления источника питания. Найти силу тока с учетом внутреннего сопротивления возможно по выражению:
I=E/Rэ = E/r0+R, где:
- E – ЭДС источника питания;
- rо – внутреннее сопротивление источника питания.
Поскольку сложная электрическая цепь, состоящая из нескольких ветвей и имеющая в своей структуре ряд устройств питания, не может быть описана законом Ома, то применяют 1-ый и 2-ой закон Кирхгофа.
Первый закон Кирхгофа
Закон Кирхгофа гласит, что сумма токов, втекающих в узел, равна сумме токов, вытекающих из него, это выглядит как:
∑mIk=0, где m – число ветвей, подведенных к узлу.
https://www.youtube.com/watch?v=LzqkLKOyid8
Согласно закону Кирхгофа, токи, втекающие в узел, используются со знаком «+», а токи, вытекающие из узла, – со знаком «-».
Второй закон Кирхгофа
Из второго закона Кирхгофа следует, что сумма падений напряжений на всех элементах цепи равна сумме ЭДС цепи, выглядит как:
∑nEk=∑mRkIk=∑mUk, где:
- n – число источников ЭДС в контуре;
- m – число элементов с сопротивлением Rk в контуре;
- Uk=RkIk – напряжение или падение напряжения на k-том элементе контура.
Перед применением второго закона Кирхгофа следует проверить выполнение следующих требований:
- Указать относительно положительные направления ЭДС, токов и напряжений;
- Указать направление обхода контура, описываемого уравнением;
- Применяя одну из трактовок 2-го закона Кирхгофа, характеристики входящие в уравнение используются со знаком «+», если их относительно положительные направления схожи с обходом контура, и с «-», если они разнонаправленные.
Из 2-го закона Кирхгофа следует выражение баланса мощностей, по которому мощность источников питания в любой момент времени равна сумме мощностей, расходуемых на всех участках цепи. Уравнение баланса мощностей имеет вид:
∑EI=∑RI2.
Метод преобразования электрической цепи
Элементы в электрических цепях могут соединяться параллельно, последовательно, смешанным способом и по схемам «звезда», «треугольник». Расчет таких схем упрощается путем замены нескольких сопротивлений на эквивалентное сопротивление, и дальнейшие вычисления уже проводятся по закону Ома либо Кирхгофа.
Последовательное и параллельное соединение элементов
Под смешанным соединением элементов подразумевается одновременное присутствие в схеме и последовательного, и параллельного соединения элементов. При этом сопротивление смешанного соединения вычисляется после преобразования схемы в эквивалентную цепь с помощью формул, приведенных на рис. выше.
Также встречается соединение элементов «звездой» и «треугольником». Для нахождения эквивалентного сопротивления необходимо первоначально преобразовать схему «треугольник» в «звезду». По картинке ниже, сопротивления равны:
- R1=R12R31/R12+R31+R23,
- R2=R12R23/R12+R31+R23,
- R3=R31R23/R12+R31+R23.
Треугольник и звезда соединений
Дополнительные методы расчета цепей
Все дополнительные методы расчета цепей в той или иной мере являются или основаны на первом и втором законах Кирхгофа. К этим методам относятся:
- Метод контурных токов – основан на введении дополнительных величин контурных токов, удовлетворяющих 1-му закону Кирхгофа;
- Метод узловых потенциалов – с его помощью находят потенциалы всех узлов схемы и затем по известным потенциалам токи во всех ветвях. Метод базируется на первом законе Кирхгофа;
- Метод эквивалентного генератора – этот метод предоставляет решение задачи, как найти ток только в одной или нескольких ветвях. Суть метода в том, что любую электрическую цепь по отношению к исследуемой ветви можно представить в виде эквивалентного генератора;
- Метод наложения – основан на том, что ток в цепи или ветви схемы равен алгебраической сумме токов, наводимых каждым источником в отдельности.
Основная часть методов расчета направлена на упрощение процедуры определения токов в ветвях схемы. Эти мероприятия проводятся либо упрощением систем уравнений, по которым проводятся расчеты, либо упрощением самой схемы. Основываясь, в первую очередь, на постулаты Кирхгофа, любой из методов отвечает на вопрос: как определить силу тока и напряжение электрической цепи.
Расчет падения напряжения в кабеле
Источник: https://elquanta.ru/teoriya/raschet-ehlektricheskikh-cepejj.html
