Как расставить направление токов в цепи?

Электротехника Часть 5 Методы расчёта электрических цепей

Всем доброго времени суток. В прошлой статье я рассматривал типы соединений приемников энергии в электрических цепях, а так же законы Кирхгофа, которые определяют основные соотношения токов и напряжений в этих цепях. Но кроме знания основных законов электротехники необходимо уметь рассчитывать неизвестные параметры электрических цепей по заданным известным параметрам. Так, например, по известным напряжениям, ЭДС и сопротивлениям необходимо знать какую мощность будет потреблять тот или иной приемник энергии, а так же вся цепь в целом. Этим мы и займёмся в данной статье.

Для сборки радиоэлектронного устройства можно преобрески DIY KIT набор по ссылке.

Расчёт электрических цепей с помощью законов Кирхгофа

Существует несколько методов расчёта электрических цепей, которые различаются между собой параметрами, которые необходимо найти, а так же количеством необходимых расчётов.

Вначале я расскажу, как произвести расчёт цепи в общем виде, но в результате размеры вычислений будут неоправданно большими. Данный метод расчёта основан на законах Ома и Кирхгофа и используется при расчётах небольших цепей с малым количеством контуров.

Для этого составляют систему уравнений из (q — 1) уравнений для узлов цепи и n уравнений для независимых контуров. Независимые контуры характеризуются тем, что при составлении уравнений для каждого нового контура входит хотя бы одна новая ветвь, не вошедшая в предыдущий контур.

В качестве примера рассчитаем электрическую цепь, приведённую на рисунке ниже

Пример электрической цепи для расчёта по законам Ома и Кирхгофа.

В качестве примера возьмём следующие параметры схемы: E1 = 50 B, E2 = 30 B, R1 = R3 = 10 Ом, R2 = R5 = 20 Ом, R4 = 25 Ом.

1. Составим уравнение по первому закону Кирхгофа. Так как узла у нас два, то выберем узел А и составим для него уравнение. Я выбрал условно, что токи I1 и I2 втекают в узел, а I3 – вытекает, тогда уравнение будет иметь вид
2. Составим недостающие уравнения по второму закону Кирхгофа. В схеме у нас два независимых контура: E1R1R2R4E2R3  и E2R4R5, поэтому выбирая произвольное направление контуров составим недостающие два уравнения. Я выбрал обход по ходу часовой стрелке, поэтому уравнения имеют вид

Таким образом, получившаяся система уравнений будет иметь следующий вид

Решив данную систему, получим следующие результаты: I1 ≈ 0,564 А, I2 ≈ 0,103 А, I2 ≈ 0,667 А.

В результате решения системы уравнений по данному методу может оказаться, что токи получились отрицательными. Это значит, что действительное направление токов противоположно по направлению выбранному.

Метод контурных токов

Рассмотренный выше метод расчета электрических цепей при анализе больших и разветвленных цепей приводит к неоправданно трудоемким расчетам, поэтому редко применяется. Более широко используется метод контурных токов, позволяющий значительно сократить количество уравнений. При этом вместо токов в ветвях электрической цепи определяются так называемые контурные токи при помощи второго закона Кирхгофа. Таким образом, количество требуемых уравнений будет равняться числу независимых контуров. В качестве примера рассчитаем цепь изображённую на рисунке ниже

Расчет цепи методом контурных токов.

Если бы мы вели расчёт цепи по методу законов Ома и Кирхгофа, то необходимо было бы решить систему из пяти уравнений. Для расчёта по методу контурных токов необходимо всего три уравнения.

В начале расчёта выделяют независимые контуры, в нашем случае это: E1R1R2E2, E2R2R4E3R3 и E3R4R5. Затем контурам присваивают произвольно направленный контурный ток, который имеет одинаковое направление для всех участков выбранного контура, в нашем случае для первого контура контурный ток будет Ia, для второго – Ib, для третьего – Ic. Как видно из рисунка некоторые контурные токи соответствуют токам в ветвях

https://www.youtube.com/watch?v=bR_cJDOMjxo

Остальные же токи можно найти как разность двух контурных токов

В результате выбора контурных токов можно составить систему уравнений по второму закону Кирхгофа

Рассчитаем схему, изображённую на рисунке выше со следующими параметрами E1 = E3 = 100 B, E2 = 50 B, R1 = R2 = 10 Ом, R3 = R4 = R5 = 20 Ом. Запишем систему уравнений

В результате решения системы получим Ia = I1 = 4,286 А, Ib = I3 = 3,571 А, Ic = I5 = -0,714 А, I2 = -0,715 А, I4 = 4,285 А. Так же как и в предыдущем случае если токи получаются отрицательными, значит действительное направление противоположно принятому. Таким образом, токи I2 и I5 имеют направление противоположное изображённым на рисунке.

Метод узловых напряжений

Кроме метода контурных токов, для уменьшения трудоемкости расчётов, применяют метод узловых напряжений, при этом возможно еще меньшее число уравнений, так как при этом методе их число достигает

где q – количество узлов в электрической цепи.

Принцип расчёта электрической цепи заключается в следующем:

1. Принимаем один из узлов цепи за базисный и присваиваем ему потенциал равный нулю;
2. Для оставшихся узлов составляем уравнения по первому закону Кирхгофа, заменяя токи в ветвях по закону Ома через напряжение и сопротивление;
3. После решения получившейся системы уравнений вычисляем токи в ветвях по обобщенному закону Ома.

В качестве примера возьмём предыдущую цепь и составим систему уравнений

Схема для решения уравнений методом узловых потенциалов.

В качестве базисного возьмём узел А и заземлим его, для остальных узлов B и D составим уравнения по первому закону Кирхгофа

Примем потенциалы узлов В = U1 и D = U2, тогда токи в ветвях выразятся через обобщённый закон Ома

В результате получившаяся система будет иметь следующий вид

Рассчитаем схему, изображённую на рисунке выше со следующими параметрами E1 = E3 = 100 B, E2 = 50 B, R1 = R2 = 10 Ом, R3 = R4 = R5 = 20 Ом. Запишем систему уравнений

В результате решения системы уравнений мы пришли к следующим результатам: потенциал в узле В – U1 = -57,14 В, а в узле D – U2 = 14,29 В. Теперь нетрудно посчитать, что токи в ветвях будут равны

Результат решения для токов I2 и I5 получился отрицательным, так как действительное направление токов противоположно направлению, изображённому на рисунке. Данные результаты совпадают с результатами, полученными для этой же схемы при расчёте по методу контурных токов.

Теория это хорошо, но без практического применения это просто слова.Здесь можно всё сделать своими руками.

Источник: https://www.electronicsblog.ru/nachinayushhim/elektrotexnika-chast-5-metody-raschyota-elektricheskix-cepej.html

1. Произвольно задать направление токов в ветвях исследуемой цепи

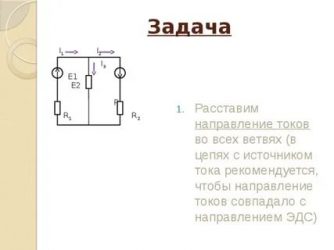
2. Исходнуюцепь, содержащую nисточников,преобразовать в nподсхем, каждая из которых содержиттолько один из источников, прочиеисточники исключаются следующим образом:источники напряжения замыкаютсянакоротко, а ветви с источниками токаобрываются. При этом необходимо помнить,что внутренние сопротивления реальныхисточников играют роль потребителей,и поэтому они должны оставаться вподсхемах.

3. Определитьтоки каждой из подсхем, задавшись ихнаправлением в соответствии с полярностьюисточника, любым из известных методов.В большинстве случаев расчет ведетсяпо закону Ома с использованием методаэквивалентных преобразований пассивныхцепей.

4. Полный токв любой ветви исходной цепи определяетсякак алгебраическая сумма токоввспомогательных подсхем, причем присуммировании со знаком «+» берутся токиподсхем, направление которых совпадаетс направлением тока в исходной цепи, сознаком «–» – остальные.

1.4.Пример расчета

1.4.1. Задание

Рассчитатьцепь, изображенную графом а,с параметрами: Е1 = 20 В;Е6 = 40 В;J3=2А;R1=R3=R5=R7=5,4 Ом; R2=R4=R6=6,8 Ом.

Подлежащаярасчету цепь будет иметь вид (рис. 1.3).

1.4.2.Запись уравнений Кирхгофа

Дляпроизвольно выбранных и обозначенныхна схеме (см. рис. 1.3) положительныхнаправлений токов ветвей и совокупностинезависимых контуров запишем:

– уравненияпо Iзакону Кирхгофа:

дляузла А:I1– I2– J3 = 0,

дляузлаВ:I7– I6– I4– I1 = 0,

дляузлаС:I4+ I2– I5 = 0,

– уравненияпо IIзакону Кирхгофа:

дляконтураI: I1R1+ I2R2– I4R4= E1,

дляконтураII: I4R4+ I5R5– I6R6= –E6,

дляконтура III:I6R6+ I7R7= E6,

дляконтура IV:J3R3– I5R5– I2R2= UJ.

Послеподстановки численных значенийкоэффициентов получаем разрешимуюсистему уравнений с семью неизвестнымивеличинами :

1.4.3. Метод контурных токов

Длярассматриваемой четырехконтурной цепи(см. рис. 1.3) система уравненийотносительно контурных токов, совпадающихпо направлению с обходом контуров,примет вид

Длявыбранных контурных токов I44= J3.Подсчитаем значения коэффициентовсистемы:

– собственныесопротивления контуров:

– общиесопротивления контуров:

– контурные ЭДС:

Послеподстановки численных значенийкоэффициентов и необходимых преобразованийсистема уравнений примет вид

Вслучае решения данной системы при помощиопределителей необходимо совместнорешить систему из первых трех уравненийотносительно неизвестных токов I11,I22,I33,а затем из четвертого уравнения системыопределить UJ.

Результатырасчета системы уравнений следующие:

Всоответствии с принятыми (см. рис.1.3)положительными направлениями токов вветвях вычисляем их значения:

1.4.3. Баланс мощности

Мощностьисточников

Мощностьпотребителей

Оценим относительнуюпогрешность расчета,

1.4.4. Метод узловых потенциалов

Принимаемпотенциал узла Аравным нулю (см. рис.1.3).Составим систему уравнений по методуузловых потенциалов относительно В,С,D:

Выпишеми подсчитаем значения коэффициентовсистемы:

– собственнаяпроводимость узлов

– общиепроводимости узлов

– узловыетоки

Система уравненийпосле подстановки численных значенийкоэффициентов примет вид

Результатырасчета системы уравнений:

Рассчитаемзначения токов в ветвях по обобщенномузакону Ома

Источник: https://studfile.net/preview/501817/page:4/

Методы расчета электрических цепей

Для правильного расчета напряжения, тока и мощности на определенных участках электрических цепей используют различные методы. Среди них выделяют:

• метод контурных токов;
• метод преобразования цепи;
• метод применения на практике законов Кирхгофа;
• метод наложения;
• метод эквивалентного генератора.

Наиболее распространенными в практике для решения поставленных задач является метод преобразования цепи и метод непосредственного применения законов Кирхгофа.

Метод преобразования электрической цепи

Суть данного метода заключается в правильном расчете распределения токов в электрической цепи. При включенных параллельно или последовательно нескольких сопротивлений можно сделать замену одним сопротивлением. Тогда распределение тока в изучаемой цепи не будет меняться.

При последовательном соединении резисторов сопротивление окажутся подключенными таким образом, что начало последующего сопротивления присоединится к концу предыдущего сопротивления. В этом случае ток во всех соединенных последовательным образом элементах будет иметь одинаковые значения.

• Курсовая работа 440 руб.
• Реферат 260 руб.
• Контрольная работа 220 руб.

Любая электрическая цепь содержит:

• приемники электроэнергии;
• источники электроэнергии.

Связь между ними осуществляется проводами. Это обеспечивает процесс протекания токов по элементам цепи. Существует два типа источников:

• источники напряжения;
• источники тока.

Идеальный источник напряжения может поддерживать в неизменном виде определенное значение напряжения в своих зажимах. Это происходит независимо от тока, который отдается в нагрузку. Внутреннее сопротивление равняется нулю.

Идеальный источник тока может обеспечить постоянное значение тока, который отдается в нагрузку. Это происходит независимо от создаваемого напряжения на его зажимах. Внутреннее сопротивление источника тока будет бесконечно большим.

Метод применения законов Кирхгофа

Токи и напряжения в любой электрической цепи подчиняются законам Кирхгофа. Это не зависит от формы и мощности сигналов, которые передают источники питания. Кроме источников питания цепь обладает резистивными элементами.

Первый закон Кирхгофа можно представить в виде алгебраической суммы всех токов, которые сходятся в одном узле цепи. Она будет равна нулю.

$\sum{i{k}{t}}=0$

При этом положительные направления токов в каждой ветви цепи имеют произвольные значения. Токи, которые направлены к узлу, принимают отрицательные значения. Токи, которые направлены от узла, принимают положительные значения.

При записи уравнения, которое характеризует метод, изучается сложная цепь. Она состоит из ветвей ($NB$), объединенных в узлы ($NY$) и ветви с источниками тока ($NJ$). В такой цепи есть резистивные элементы, источники тока, источники электродвижущей силы.

При анализе цепи на основании закона Кирхгофа можно определить число неизвестных токов, указать положительное направление тока в каждой ветви цепи, а также составить ряд независимых уравнений.

Для этого используется топологический граф схемы цепи. При изображении ветвей графа различают, к какому типу ветви она приходит на замену. При составлении расчетов принято изображать первый тип в виде сплошной линии.

Для ветви второго типа, в которой значение тока определяется самим источником тока, используется пунктирная линия.

Ветви графа $NB$ и узлы $NY$ нумеруют также, как и номера ветвей схемы и узлов исходной цепи. Ориентация ветвей графа будет соответствовать направлениям напряжений и токов исходной цепи. В канонической ветви первого типа напряжение и ток выбираются всегда по направлению, которые совпадают между собой, поэтому они ориентируется на ветвь графа. Вырожденной ветвью называется та, где содержится только источник напряжения. Ее ориентация в графе производится по напряжению источника и направляется против действия электродвижущей силы.

Анализ топологического графа принято начинать с выделения ветвей дерева графа ($N_Д$) и ветвей связи ($NC$). Все ветви дерева образуют связный подграф. Он объединяет все узлы, где нет замкнутого контура. Выбор ветвей дерева осуществляется в произвольном порядке. В него не могут включать ветви графа, которые замещают источники тока.

Определение 1

Ветви связи являются дополнением к ветвям дерева. Присоединение новой ветви связи к существующим ветвям дерева формирует замкнутый контур. Он называется главным контуром.

Число независимых уравнений $N_1$, которые могут быть составлены по первому закону Кирхгофа, должны соответствовать числу ветвей дерева $N_Д$. Иными словами, определяется числом узлов без единицы:

$N_1 = N_Д = NY – 1$

$N_2 = N_Н — N_Д = (NB — NJ) — N_1 = NB — NJ — NY + 1$

В этом уравнении $N_Н — N_Д = (NB — NJ)$ – количество ветвей с неизвестными токами, а $NJ$ – это количество ветвей, где известны источники тока.

К системе, которая состоит из $N_Н = (N_1+ N_2)$ добавляют уравнения, связывающие напряжение и ток в каждой отдельной ветви. Их называют компонентными уравнениями.

Иные методы расчета

Также используют другие методы расчета электрических цепей.

Метод узловых потенциалов позволяет сократить порядок системы для расчета электротехнических схем. Такой способ состоит в нахождении потенциалов всех узлов схемы, а также по известным потенциалам токов во всех ветвях. Метод узловых потенциалов базируется на первом законе Кирхгофа.

https://www.youtube.com/watch?v=LzqkLKOyid8

Метод контурных токов основан на введении дополнительных величин контурных токов. Они должны удовлетворять первому закону Кирхгофа.

https://www.youtube.com/watch?v=LzqkLKOyid8

Метод эквивалентного генератора применяется при определении токов в одной или нескольких ветвях. Этот метод еще называют теоремой об активном двухполюснике.

Источник: https://spravochnick.ru/fizika/elektricheskie_cepi_-_chto_eto/metody_rascheta_elektricheskih_cepey/