В чем измеряется полная мощность цепи?

Формула мощности электрического тока, расчет по мощности и напряжению

Для того, чтобы обеспечить безопасность при эксплуатации промышленных и бытовых электрических приборов, необходимо правильно вычислить сечение питающей проводки и кабеля. Ошибочный выбор сечения жил кабеля может привести из-за короткого замыкания к возгоранию проводки и к возникновению пожара в здании.

Что такое мощность (Р) электротока

Электрическая мощность является физической величиной, характеризующей скорость преобразования или передачи электрической энергии. Единицей измерения по Международной системе единиц (СИ) является ватт, в нашей стране обозначается Вт, международное обозначение — W.

Что влияет на мощность тока

На мощность (Р) влияет величина силы тока и величина приложенного напряжения. Расчет параметров электроэнергии выполняется еще на стадии проектирования электрических сетей объекта. Полученные данные позволяют правильно выбрать питающий кабель, к которому будут подключаться потребители. Для расчетов силы электротока используется значения напряжения сети и полной нагрузки электрических приборов. В соответствии с величиной силы электротока выбирается сечение жил кабелей и проводов.

Отличия мощности при постоянном и переменном напряжении

Ведем обозначения электрических величин, которые приняты в нашей стране:

• Р − активная мощность, измеряется в ваттах, обозначается Вт;
• Q − реактивная мощность, измеряется в вольт амперах реактивных, обозначается ВАр;
• S − полная мощность, измеряется в вольт амперах, обозначается ВА;
• U − напряжение, измеряется в вольтах, обозначается ВА;
• I − ток, измеряется в амперах, обозначается А;
• R − сопротивление, измеряется в омах, обозначается Ом.

Назовем основные отличия P на постоянном и Q на переменном электротоке. Расчет P на постоянном электротоке получается наиболее простым. Для участков электрической цепи справедлив закон Ома. В этом законе задействованы только величина приложенного U (напряжения) и величина сопротивления R.

Расчет S (полной мощности) на переменном электротоке производится несколько сложнее. Кроме P, имеется Q и вводится понятие коэффициента мощности. Алгебраически складывая активную P и реактивную Q, получают общую S.

Расчет силы тока по мощности и напряжению в сети постоянного тока

Для расчета силы I (тока), надо величину U (напряжения) разделить на величину сопротивления.

Расчет силы тока по мощности и напряжению:

I = U ÷ R

Измеряется в амперах.

Для такого случая электрическую Р (активную мощность) можно посчитать как произведение силы электрического I на величину U.

Формула расчета мощности по току и напряжению:

P = U × I

Все компоненты в этих двух формулах характерны для постоянного электротока и их называют активными.

P = I2 × R

P = U2 ÷ R

Однофазные нагрузки

В однофазных сетях переменного электротока требуется произвести вычисление отдельно для Р и Q нагрузки, затем надо при помощи векторного исчисления их сложить.

В скалярном виде это будет выглядеть так:

S = √P2 + Q2

В результате расчет P, Q, S имеет вид прямоугольного треугольника. Два катета этого треугольника представляют собой P и Q составляющие, а гипотенуза — их алгебраическую сумму.

S измеряется в вольт-амперах (ВА), Q измеряется в вольт-амперах-реактивных (ВАр), Р измеряется в ваттах (Вт).

Зная величины катетов для треугольников, можно рассчитать коэффициент мощности (cos φ). Как это сделать, показано на изображении треугольника.

Расчет в трехфазной сети

Переменный I (ток) отличается от постоянного по всем параметрам, особенно наличием нескольких фаз. Расчет P в трехфазной нагрузке необходим для правильного определения характеристик подключаемой нагрузки. Трехфазные сети широко применяются в связи с удобством эксплуатации и малыми материальными затратами.

Трехфазные цепи могут соединяться двумя способами – звездой и треугольником. На всех схемах фазы обозначают символами А, В, С. Нейтральный провод обозначают символом N.

При соединении звездой различают два вида U (напряжения) – фазное и линейное. Фазное U определяется как U между фазой и нейтральным проводом. Линейное U определяется как U между двумя фазами.

Эти два U связаны между собой соотношением:

UЛ = UФ × √3

Линейные и фазные электротоки при соединении звездой равны друг другу: IЛ = IФ

Форма расчета S при соединении звездой:

S = SA + SB + SC = 3 × U × I

Активная P:

Р = 3 × Uф × Iф × cosφ

Реактивная Q:

Q = √3 × Uф × Iф × sinφ.

При соединении треугольником фазное и линейное U равны друг другу: UЛ = UФ

Линейный I при соединении треугольником определяется по формуле:

IЛ = IФ × √3

Формулы мощности электрического тока при соединении треугольником:

• S = 3 × Sф = √3 × Uф × Iф;
• Р = √3 × Uф × Iф × cosφ;
• Q = √3 × Uф × Iф × sinφ.

Средняя P в активной нагрузке

В электрических сетях P измеряют при помощи специального прибора – ваттметра. Схемы подключения находятся в зависимости от способа подключения нагрузки.

При симметричной нагрузке P измеряется в одной фазе, а полученный результат умножают на три. В случае несимметричной нагрузки для измерения потребуется три прибора.

Параметры P электросети или установки являются важными данными электрического прибора. Данные по потреблению P активного типа передаются за определенный период времени, то есть передается средняя потребляемая P за расчетный период времени.

Подбор номинала автоматического выключателя

Автоматические выключатели защищают электрические аппараты от токов короткого замыкания и перегрузок.

При аварийном режиме они обесточивают защищаемую цепь при помощи теплового или электромагнитного механизма расцепления.

Тепловой расцепитель состоит из биметаллической пластины с различными коэффициентами теплового расширения. Если номинальный ток превышен, пластина изгибается и приводит в действие механизм расцепления.

Минимальный I, при котором тепловой расцепитель должен сработать, устанавливается с помощью регулировочного винта.

Ток срабатывания у электромагнитного расцепителя при коротком замыкании равен произведению установленного срабатывания на номинальный электроток расцепителя.

о законах электротехники

Из следующего видео можно узнать, что такое электричество, мощность электрического тока. Даны примеры практического применения законов электротехники.

Источник: https://vdome.club/materialy/raschety/formula-moschnosti.html

В чем измеряется полная мощность цепи

В электротехнике среди множества определений довольно часто используются такие понятия, как активная, реактивная и полная мощность. Эти параметры напрямую связаны с током и напряжением в замкнутой электрической цепи, когда включены какие-либо потребители.

Для проведения вычислений применяются различные формулы, среди которых основной является произведение напряжения и силы тока. Прежде всего это касается постоянного напряжения. Однако в цепях переменного тока мощность разделяется на несколько составляющих, отмеченных выше.

Вычисление каждой из них также осуществляется с помощью формул, благодаря которым можно получить точные результаты.

Формулы активной, реактивной и полной мощности

Основной составляющей считается активная мощность. Она представляет собой величину, характеризующую процесс преобразования электрической энергии в другие виды энергии. То есть по-другому является скоростью, с какой потребляется электроэнергия. Именно это значение отображается на электросчетчике и оплачивается потребителями. Вычисление активной мощности выполняется по формуле: P = U x I x cosф.

В отличие от активной, которая относится к той энергии, которая непосредственно потребляется электроприборами и преобразуется в другие виды энергии – тепловую, световую, механическую и т.д., реактивная мощность является своеобразным невидимым помощником. С ее участием создаются электромагнитные поля, потребляемые электродвигателями. Прежде всего она определяет характер нагрузки, и может не только генерироваться, но и потребляться. Расчеты реактивной мощности производятся по формуле: Q = U x I x sinф.

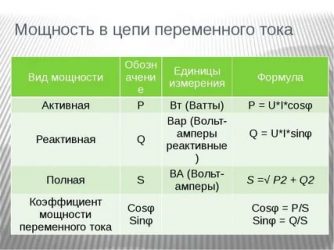
Полной мощностью является величина, состоящая из активной и реактивной составляющих. Именно она обеспечивает потребителям необходимое количество электроэнергии и поддерживает их в рабочем состоянии. Для ее расчетов применяется формула: S = .

Как найти активную, реактивную и полную мощность

Активная мощность относится к энергии, которая необратимо расходуется источником за единицу времени для выполнения потребителем какой-либо полезной работы. В процессе потребления, как уже было отмечено, она преобразуется в другие виды энергии.

В цепи переменного тока значение активной мощности определяется, как средний показатель мгновенной мощности за установленный период времени. Следовательно, среднее значение за этот период будет зависеть от угла сдвига фаз между током и напряжением и не будет равной нулю, при условии присутствия на данном участке цепи активного сопротивления. Последний фактор и определяет название активной мощности. Именно через активное сопротивление электроэнергия необратимо преобразуется в другие виды энергии.

При выполнении расчетов электрических цепей широко используется понятие реактивной мощности. С ее участием происходят такие процессы, как обмен энергией между источниками и реактивными элементами цепи. Данный параметр численно будет равен амплитуде, которой обладает переменная составляющая мгновенной мощности цепи.

Существует определенная зависимость реактивной мощности от знака угла ф, отображенного на рисунке. В связи с этим, она будет иметь положительное или отрицательное значение. В отличие от активной мощности, измеряемой в ваттах, реактивная мощность измеряется в вар – вольт-амперах реактивных. Итоговое значение реактивной мощности в разветвленных электрических цепях представляет собой алгебраическую сумму таких же мощностей у каждого элемента цепи с учетом их индивидуальных характеристик.

Основной составляющей полной мощности является максимально возможная активная мощность при заранее известных токе и напряжении. При этом, cosф равен 1, когда отсутствует сдвиг фаз между током и напряжением. В состав полной мощности входит и реактивная составляющая, что хорошо видно из формулы, представленной выше. Единицей измерения данного параметра служит вольт-ампер (ВА).

Активная мощность вычисляется по формуле:

(2.20)

Активную мощность потребляет резистивный элемент. Единица измерения активной мощности называется Ватт (Вт), производная единица – килоВатт (кВт), равная 10 3 Вт.

Реактивная мощность вычисляется по формуле:

(2.21)

Реактивная мощность потребляется идеальным индуктивным и

емкостным элементами. Единица измерения реактивной мощности называется Вольт-Ампер реактивный (Вар), производная единица – килоВАр (кВАр), равная 10 3 ВАр.

Полная мощность потребляется полным сопротивлением и обозначается буквой S:

Источник: https://vemiru.ru/info/v-chem-izmerjaetsja-polnaja-moshhnost-cepi/

Мощность переменного тока — виды, формула, примеры вычисления

Электрическое напряжение определяется как отношение работы поля по переброске пробного заряда из одной заданной точки в другую к размеру потенциала. При дислокации единичного резерва выполняется работа, которая равняется напряжению на искомом участке. Общая мощность получают умножением работы электрического поля для единичного заряда на число потенциалов за определенную единицу времени.

В переменной электрической цепи выделяется 3 вида мощности:

• активный P;
• реактивный Q;
• полного типа S.

В цепи переменного электричества формула для расчета постоянного тока применяется только для вычисления мгновенной мощности. Этот показатель претерпевает изменения во времени и почти не имеет практического смысла для всех остальных расчетов. Среднезначимый показатель мощности требует временной интеграции. Мгновенная мощность объединяется в течение определенного промежутка для расчета величины в магистрали с периодическим изменением силы переменного потока и синусоидального напряжения.

Применяется концепция комплексных чисел для связывания всех трех видов мощности. Это понятие обозначает, что в переменной цепи нагрузка выражается подобным числом так, что активная разновидность представляется действительной составляющей. Реактивный показатель выступает мнимым показателем, а полная мощность показывается в форме модуля. В этих расчетах принимает участие угол сдвига фаз φ, который является аргументом баланса мощностей в цепи переменного тока.

Активная мощность

Активная скорость преобразования выражается также через взаимное отношение силы потока, напряжения к значению активной составляющей сопротивления. В магистрали синусоидального и несинусоидального движения электронов активная нагрузка приравнивается к сумме аналогичных значений на отдельных участках.

Для определения среднего периодического размера используется активная мощность переменного тока, формула расчета P = U . I . cos φ (косинус), где:

1. U — мощность.
2. I — сила потока.
3. φ — угол смещения фаз.

Средний показатель мгновенной скорости преобразования в однофазной цепи берется в виде среднеквадратичного значения тока и напряжения с определенным углом сдвига. В цепях несинусоидального электричества мощность приравнивается к сумме соответствующих показателей отдельных перемещений. С помощью активной мощности характеризуется интенсивность необратимого видоизменения электроэнергии в другие разновидности, например, электромагнитную или тепловую.

Проходящая мощность используется в качестве активной в концепции длинных магистралей для анализа электромагнитных течений, протяженность которых сопоставляется с размерностью волны. Искомое значение рассчитывается как разница между понижающейся и отражающейся мощностями. От свойств коэффициента углового смещения зависят полученные показатели отрицательной или положительной нагрузки активного типа.

Реактивная характеристика

Для обозначения применяется дополнительно единица вольт-ампер реактивный (вар). В русских аналогах используется вар, а международные специалисты применяют var. В РФ единица допускается для электротехнических расчетов в форме внесистемного значения.

Нахождение производится по формуле P = U . I . sin φ (синус), где:

1. U — среднеквадратичная мощность.
2. I — среднеквадратичная сила потока.
3. φ — угол фазного смещения, значения синуса, определяются по таблицам.

При диапазоне показателя от 0 до 90º (ток отстает от напряжения, а нагрузка носит активно-индуктивный вид) синус φ будет иметь положительное значение. При угловом сдвиге от 0 до -90º (поток электронов опережает нагрузку, мощность отличается активно-емкостным свойством) константа всегда показывает отрицательный знак. Реактивная мощность характеризует напряженность, которая возникает в электромеханических приборах и цепях при изменении энергетических волн поля в магистрали переменного синусоидального потока.

В физическом смысле реактивная нагрузка показывает энергию, которая перекачивается от источника тока на конденсаторы, индукторы, двигательные обмотки, а впоследствии возвращается к источнику за один колебательный период. Реактивная мощность не принимает участия в работе электротока. В случае положительной характеристики устройство потребляет, а нагрузка с отрицательным знаком говорит о производстве энергии.

Это обстоятельство рассматривается в условном контексте, т. к. почти все энергопотребляющие приборы, например, двигатели асинхронной работы, а также полезная нагрузка, подаваемая через трансформатор, относятся к активно-индуктивным видам. Синхронные двигатели электростанций одновременно производят и потребляют энергию в зависимости от максимальной величины электротока возбуждения в роторных обмотках. Эта особенность применяется для координации уровня нагрузки в магистрали в электротехнике.

С помощью современных преобразователей производится компенсация реактивной нагрузки во избежание перегрузок и для увеличения коэффициента мощности электроустановок. Приборы более точно оценивают размер энергии, которая поступает в обратном направлении от индуктора к источнику переменного тока.

Полная нагрузка

Показатель используется в физике для описания потребляемой мощности, которая прилагается к подводящим агрегатам электросети с использованием резисторов. Суммируются параметры ЭДС распределительных щитков, кабелей, проводов, ЛЭП, трансформаторов.

Полную нагрузку можно рассчитать по формуле S = U . I, где:

1. S — параметр полной нагрузки (В/а).
2. U — расчетная нагрузка в генераторе.
3. I — комплексный показатель силы тока в сочетании с обмоточным значением.

Параметр темпа преобразований зависит от характеристик применяемого тока, а не от свойств фактически использованной нагрузки. По этой причине полная мощность распределительных электрощитов и трансформаторных агрегатов измеряется в вольт-амперах, а значение ватт к ней не применяется.

Работа в различных условиях

Модуль комплексного показателя интенсивности передвижения равняется показателю полной нагрузки. Действительная составляющая часть приравнивается к активной силе, а мнимая считается реактивным видом. Имеет место положительный или отрицательный знак, что зависит от интенсивности загруженности цепи. Комплексная мощность должна соответствовать сопряженному электрическому сопротивлению. Положительная нагрузка характеризуется соотношением Р > 0, а знак минус проявляется в случае Р < 0.

Измерение мощностных характеристик переменного потока электронов проводится при пропускании равного по значению тока по фазным проводникам. Показатели силы течения заряженных частиц с применением нулевого проводника имеют ничтожную размерность. Равномерная или симметричная фазовая нагрузка в трехфазной магистрали зависит от величины протекающих токов. Неравномерная или несимметричная нагрузка зависит от прохождения потока по нейтральным или нулевым кабелям. Общий мощностной уровень находится суммированием.

Если присутствует фазовый сдвиг между напряжением и силой тока, то он совпадает с углом смещения между векторными радиусами показателей электротока. В условиях переменного напряжения совпадение векторных радиусов тока и вольтажа отмечается только при отсутствии в цепи конденсаторов и катушек индукции. Установка индукторов не мешает совпадению фазных значений. При этом происходит векторное вращение равной интенсивности. График смещения внутреннего угла остается постоянным.

Если в магистрали происходит сдвиг напряжения и переменного тока, то мощностные показатели представляются значением с отрицательным знаком, так как калькулятор перемножает положительные и отрицательные величины. Продолжительность периодов зависит от уровня смещения фаз. При этом длительность отрицательных нагрузок определяет характеристики сдвига. При расчетах используются показатели сопротивления, которые знакомы из физического закона Ома.

Коэффициент скорости преобразования

Мощностной коэффициент является показателем потребления тока при присутствии реактивного компонента и искажающей нагрузки. Значение коэффициента отличается от понятия косинуса сдвигаемого угла. Второе понятие характеризуется смещением протекающего переменного тока, напряжения и используется только при синусоидальном токе и силе равного значения.

Коэффициент равняется отношению расходуемой нагрузки к ее полному значению. При этом работа совершается за счет активного вида преобразования. При синусоидальном токе и вольтаже полная нагрузка находится в виде суммы реактивной и активной форм. Активная нагрузка приравнивается к усредненному произведению силы тока и напряжения и не может быть выше произведения аналогичных среднеквадратических размерностей. Мощностной коэффициент показывается в диапазоне от 0 до 1 или ставится в процентах от 0 до 100.

Если реактивный элемент присутствует в нагрузке, то, помимо мощностного коэффициента, указывается характер работы (емкостно-активный или индуктивно-активный). Коэффициент в этих случаях отличается и является отстающим или опережающим значением.

Практическое применение и коррекция

Если к розетке с синусоидальным напряжением 50 Гц и 230 В подсоединить нагрузку с опережением или отставанием тока от напряжения на какую-то угловую величину, то на активной внутренней катушке будет создаваться увеличенная мощность. Это значит, что при работе в таких условиях выделяется много тепла, и электростанция отводит его в увеличенном количестве, по сравнению с применением активной нагрузки.

Коэффициенты полезного действия и мощности отличаются друг от друга. Мощностной показатель не влияет на потребление приемника, подключенного к сети, но изменяет энергетические потери в подводных проводах и местах выработки энергии или ее преобразования. В доме электросчетчик не реагирует на проявление мощности, так как оплачивается только та энергия, за счет которой работают приборы.

КПД влияет на потребляемую активную нагрузку. Например, энергосберегающая лампа потребляет в полтора раза больше электричества, чем аналогичный прибор накаливания. Это говорит о высоком коэффициенте полезного действия у первой лампы. Но показатель нагрузки может быть низким и высоким в обоих вариантах.

Коррекция заключается в приведении потребления прибора с низким мощностным коэффициентом к стандартным показателям при питании от силовой цепи переменного тока. Технически это осуществляется применением действенной схемы на входном устройстве, которая помогает равномерно использовать фазную мощность и исключает перегрузку нулевого провода. При этом снижаются всплески потребительского тока на верхушке синусоиды питающего вольтажа.

Реактивная нагрузка корректируется при включении в магистраль элемента с обратным действием. Например, в двигателе переменного тока для компенсации действия ставится конденсатор параллельно питающей линии. Применяется система активного или пассивного корректора при изменении используемого тока во время колебательного периода подпитывающего напряжения для преобразования коэффициента. Простым примером является последовательное подключение дросселя. При этом конечные приборы потребляют ток непропорционально гармоничным искажениям. Катушка сглаживает волновые импульсы.

Источник: https://nauka.club/fizika/moshchnost-peremennogo-toka.html

Мощность переменного тока

Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: переменный ток, вынужденные электромагнитные колебания

Переменный ток несёт энергию. Поэтому крайне важным является вопрос о мощности в цепи переменного тока.

Пусть и — мгновенные значение напряжения и силы тока на данном участке цепи. Возьмём малый интервал времени — настолько малый, что напряжение и ток не успеют за это время сколько-нибудь измениться; иными словами, величины и можно считать постоянными в течение интервала .

Пусть за время через наш участок прошёл заряд (в соответствии с правилом выбора знака для силы тока заряд считается положительным, если он переносится в положительном направлении, и отрицательным в противном случае). Электрическое поле движущихся зарядов совершило при этом работу

(1)

Точно такую же формулу мы получили в своё время для постоянного тока. Но в данном случае мощность зависит от времени, совершая колебания вместе током и напряжением; поэтому величина (1) называется ещё мгновенной мощностью.

Из-за наличия сдвига фаз сила тока и напряжение на участке не обязаны совпадать по знаку (например, может случиться так, что напряжение положительно, а сила тока отрицательна, или наоборот). Соответственно, мощность может быть как положительной, так и отрицательной. Рассмотрим чуть подробнее оба этих случая.

1. Мощность положительна: . Напряжение и сила тока имеют одинаковые знаки. Это означает, что направление тока совпадает с направлением электрического поля зарядов, образующих ток. В таком случае энергия участка возрастает: она поступает на данный участок из внешней цепи (например, конденсатор заряжается).

2. Мощность отрицательна: . Напряжение и сила тока имеют разные знаки. Стало быть, ток течёт против поля движущихся зарядов, образующих этот самый ток.

Как такое может случиться? Очень просто: электрическое поле, возникающее на участке, как бы «перевешивает» поле движущихся зарядов и «продавливает» ток против этого поля. В таком случае энергия участка убывает: участок отдаёт энергию во внешнюю цепь (например, конденсатор разряжается).

Если вы не вполне поняли, о чём только что шла речь, не переживайте — дальше будут конкретные примеры, на которых вы всё и увидите.

Мощность тока через резистор

Пусть переменный ток протекает через резистор сопротивлением . Напряжение на резисторе, как нам известно, колеблется в фазе с током:

Поэтому для мгновенной мощности получаем:

(2)

График зависимости мощности (2) от времени представлен на рис. 1. Мы видим, что мощность всё время неотрицательна — резистор забирает энергию из цепи, но не возвращает её обратно в цепь.

Рис. 1. Мощность переменного тока через резистор

Максимальное значение нашей мощности связано с амплитудами тока и напряжения привычными формулами:

Посмотрите ещё раз внимательно на рис. 1. Не возникает ли у вас интуитивное ощущение, что средняя мощность соответствует «середине» нашей синусоиды и принимает поэтому значение ?

Это ощущение совершенно верное! Так оно и есть. Разумеется, можно дать математически строгое определение среднего значения функции (в виде некоторого интеграла) и подтвердить нашу догадку прямым вычислением, но нам это не нужно. Достаточно интуитивного понимания простого и важного факта:

среднее значение квадрата синуса (или косинуса) за период равно .

Этот факт иллюстрируется рисунком 2.

Рис. 2. Среднее значение квадрата синуса равно

Итак, для среднего значения мощности тока на резисторе имеем:

(3)

В связи с этими формулами вводятся так называемые действующие (или эффективные) значения напряжения и силы тока (на самом деле это есть не что иное, как средние квадратические значения напряжения и тока. Такое у нас уже встречалось: средняя квадратическая скорость молекул идеального газа (листок «Уравнение состояния идеального газа»):

(4)

Поэтому если вы возьмёте лампочку, подключите её сначала к источнику постоянного напряжения , а затем к источнику переменного напряжения с таким же действующим значением , то в обоих случаях лампочка будет гореть одинаково ярко.

Действующие значения (4) чрезвычайно важны для практики. Оказывается, вольтметры и амперметры переменного тока показывают именно действующие значения (так уж они устроены). Знайте также, что пресловутые вольт из розетки — это действующее значение напряжения бытовой электросети.

Мощность тока через конденсатор

Пусть на конденсатор подано переменное напряжение . Как мы знаем, ток через конденсатор опережает по фазе напряжение на :

Для мгновенной мощности получаем:

График зависимости мгновенной мощности от времени представлен на рис. 3.

Рис. 3. Мощность переменного тока через конденсатор

Чему равно среднее значение мощности? Оно соответствует «середине» синусоиды и в данном случае равно нулю! Мы видим это сейчас как математический факт. Но интересно было бы с физической точки зрения понять, почему мощность тока через конденсатор оказывается нулевой.

Для этого давайте нарисуем графики напряжения и силы тока в конденсаторе на протяжении одного периода колебаний (рис. 4).

Рис. 4. Напряжение на конденсаторе и сила тока через него

Рассмотрим последовательно все четыре четверти периода.

Мгновенная мощность положительна: конденсатор накапливает энергию, поступающую из внешней цепи. Эта энергия возникает за счёт работы внешнего электрического поля, продвигающего заряды на конденсатор.

2. Вторая четверть, . Напряжение продолжает оставаться положительным, но идёт на убыль. Ток меняет направление и становится отрицательным: конденсатор разряжается против направления внешнего электрического поля.В конце второй четверти конденсатор полностью разряжен.

Мгновенная мощность отрицательна: конденсатор отдаёт энергию. Эта энергия возвращается в цепь: она идёт на совершение работы против электрического поля внешней цепи (конденсатор как бы «продавливает» заряды в направлении, противоположном тому, в котором внешнее поле «хочет» их двигать).

3. Третья четверть, . Внешнее электрическое поле меняет направление: напряжение отрицательно и возрастает по модулю. Сила тока отрицательна: идёт зарядка конденсатора в отрицательном направлении.

Ситуация полностью аналогична первой четверти, только знаки напряжения и тока — противоположные. Мощность положительна: конденсатор вновь накапливает энергию.

4. Четвёртая четверть, . Напряжение отрицательно и убывает по модулю. Конденсатор разряжается против внешнего поля: сила тока положительна.

Мы видим, что энергия, забранная конденсатором из внешней цепи в ходе первой четверти периода колебаний, полностью возвращается в цепь в ходе второй четверти. Затем этот процесс повторяется вновь и вновь. Вот почему средняя мощность, потребляемая конденсатором, оказывается нулевой.

Мощность тока через катушку

Пусть на катушку подано переменное напряжение . Ток через катушку отстаёт по фазе от напряжения на :

Для мгновенной мощности получаем:

Снова средняя мощность оказывается равной нулю. Причины этого, в общем-то, те же, что и в случае с конденсатором. Рассмотрим графики напряжения и силы тока через катушку за период (рис. 5).

Рис. 5. Напряжение на катушке и сила тока через неё

Мы видим, что в течение второй и четвёртой четвертей периода энергия поступает в катушку из внешней цепи. В самом деле, напряжение и сила тока имеют одинаковые знаки, сила тока возрастает по модулю; для создания тока внешнее электрическое поле совершает работу против вихревого электрического поля, и эта работа идёт на увеличение энергии магнитного поля катушки.

В первой и третьей четвертях периода напряжение и сила тока имеют разные знаки: катушка возвращает энергию в цепь. Вихревое электрическое поле, поддерживающее убывающий ток, двигает заряды против внешнего электрического поля и совершает тем самым положительную работу. А за счёт чего совершается эта работа? За счёт энергии, накопленной ранее в катушке.

Таким образом, энергия, запасаемая в катушке за одну четверть периода, полностью возвращается в цепь в ходе следующей четверти. Поэтому средняя мощность, потребляемая катушкой, оказывается равной нулю.

Мощность тока на произвольном участке

Теперь рассмотрим самый общий случай. Пусть имеется произвольный участок цепи — он может содержать резисторы, конденсаторы, катушки…На этот участок подано переменное напряжение .

Как мы знаем из предыдущего листка «Переменный ток. 2», между напряжением и силой тока на данном участке имеется некоторый сдвиг фаз . Мы записывали это так:

Тогда для мгновенной мощности имеем:

(5)

Теперь нам хотелось бы определить, чему равна средняя мощность. Для этого мы преобразуем выражение (5), используя формулу:

В результате получим:

(6)

(7)

Данную формулу можно записать с помощью действующих значений (4) напряжения и силы тока:

Формула (7) охватывает все три рассмотренные выше ситуации. В случае резистора имеем , и мы приходим к формуле (3). Для конденсатора и катушки , и средняя мощность равна нулю.

Кроме того, формула (7) даёт представление о весьма общей проблеме, связанной с передачей электроэнергии. Чрезвычайно важно, чтобы у потребителя был как можно ближе к единице. Иначе потребитель начнёт возвращать значительную часть энергии назад в сеть (что ему совсем невыгодно), и к тому же возвращаемая энергия будет безвозвратно расходоваться на нагревание проводов и других элементов цепи.

Источник: https://ege-study.ru/ru/ege/materialy/fizika/moshhnost-peremennogo-toka/

Активная и реактивная мощность 2020

Питание — это комбинация напряжения и тока в электрических цепях. С технической точки зрения, это скорость передачи электрической энергии электрическими цепями, что означает скорость передачи энергии. Аббревиатуры AC и DC часто используются в системах электропитания в качестве переменного тока и постоянного тока соответственно.

Оба представляют собой разные типы тока, используемые для передачи электрической энергии. Активная мощность и реактивная мощность являются двумя наиболее распространенными терминами, используемыми для описания потока энергии в электроэнергетических системах. Активная мощность — это реальная мощность, тогда как реактивная мощность используется для передачи реальной мощности.

В этой статье освещаются некоторые ключевые различия между ними.

Что такое активная сила?

В простых цепях переменного тока напряжение и ток являются синусоидальными, что означает, что форма волны имеет близкое сходство с идеальной синусоидальной волной.

В случае чисто резистивной нагрузки напряжение и ток изменяют свою полярность в одно и то же время и в каждый момент времени, это значение положительно означает, что направление тока не меняется в обратном направлении. В этом случае передается только активная мощность.

Активная мощность или реальная мощность — это мощность, которая фактически потребляется в цепи переменного тока. Проще говоря, рассеиваемая мощность называется активной силой. Он обозначается заглавной буквой «P» и измеряется в ваттах (W) в основном киловатт (KW) и мегаватт (МВт).

Что такое реактивная сила?

В случае чисто реактивной нагрузки напряжение не соответствует фазе тока. Произведение напряжения и тока положительно для половины каждого цикла, тогда как для другой половины цикла значение отрицательно, так как мощность непрерывно протекает между источником и нагрузкой.

Это приводит к тому, что реактивная мощность передается на нагрузку. Проще говоря, реактивная мощность — это неиспользуемая мощность или мнимая мощность, которая не используется для какой-либо полезной работы, и существует, когда напряжение и ток не соответствуют фазе.

Он обозначается заглавной буквой «Q» и измеряется вольтамперной реактивной (var) в отличие от единицы мощности СИ, которая является ваттом.

Разница между активной и реактивной мощностью

В электрических системах переменного тока величина мощности, используемой для создания эффективной работы, означающая количество мощности, которое фактически передается нагрузке, такой как трансформатор, называется «активной мощностью» или «реальной мощностью» или «истинной мощностью».

Это полезная сила, которая фактически натягивается нагрузкой в ​​результате рассеивания энергии в виде тепла.

С другой стороны, реактивная мощность — это мощность, которая непрерывно отскакивает назад и вперед между источником и нагрузкой, что означает мощность, которая не может использоваться для эффективной работы в цепи переменного тока или в системе.

Ватт является общей единицей для всех видов мощности, которая символизируется как «W», но блок обычно зарезервирован для активной мощности. Он практически измеряется в киловаттах (кВт) и мегаваттах (МВт) в электроэнергетических системах. Реактивная мощность — это форма мощности, но она не выражается в ваттах. Вместо этого он выражается реактивным вольт-амперным реактивным (var) в электроэнергетических системах переменного тока. Он обычно существует, когда форма волны тока и сигнал напряжения не соответствуют фазе, обычно на 90 градусов. Термин «вар» широко используется во всей энергетике.

Активная мощность или реальная мощность символизируется заглавной буквой «P», тогда как реактивная мощность обозначается заглавной буквой «Q». Активная мощность — это реальная мощность, рассеиваемая на нагрузках, которые затем преобразуются в другие виды энергии. В цепи переменного тока, если приложенное напряжение равно «V», а оборотным током «I», тогда среднее значение активной мощности равно P = VI cos φ, где φ — фазовый угол между током и напряжением. Формула для реактивной мощности Q = VI sin φ, где «I sin φ» здесь представляет ток, не соответствует фазе с напряжением.

Активная мощность — это сила, проявляющаяся в различных физических формах, таких как электромагнитное излучение или механическая форма или акустические волны, если на то пошло. Рассмотрим пример колеса-кургана, маленькой ручной тележки с одним колесом и предназначенной для толкания одного человека.

Реактивная мощность используется для управления напряжением во многих промышленных средах для преодоления колебаний уровней напряжения.

Резюме Активные против реактивной мощности

В цепях переменного тока активная мощность — это реальная мощность, потребляемая оборудованием для полезной работы, означающая мощность, рассеиваемую нагрузкой, тогда как реактивная мощность — это воображаемая мощность, которая не используется непосредственно для работы.

Вместо этого он постоянно отскакивает назад и вперед, что приводит к рассеянию тока, а ток, возвращающийся назад, никогда не используется для какой-либо полезной работы и который называется реактивной мощностью. Активная мощность измеряется в киловаттах (KW) или мегаваттах (MW), тогда как реактивная мощность измеряется вольтамперной реактивной (var).

Активная мощность является синфазной с нагрузкой, тогда как реактивная мощность не соответствует фазе нагрузки.

Источник: https://ru.esdifferent.com/difference-between-active-and-reactive-power

Активная, реактивная и полная мощность: формула, измерение, в чём измеряются показатели

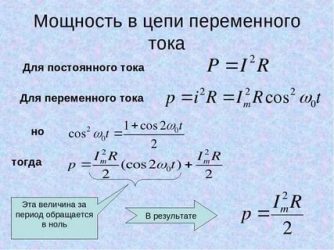
Мощность является важным фактором для оценки эффективности работы электрооборудования в сети энергосистемы. Использование её предельных значений может привести к перегрузкам сети, аварийным ситуациям и выходу оборудования из строя. Для того чтобы обезопасить себя от этих негативных последствий, необходимо понимать, что такое активная реактивная и полная мощность.

Мощность, которая фактически потребляется или используется в цепи переменного тока, называется активной, в кВт или МВт. Мощность, которая постоянно меняет направление и движется, как по направлению в цепи, так и реагирует сама на себя, называется реактивной, в киловольт (kVAR) или MVAR.

Очевидно, что мощность потребляется только при сопротивлении. Чистый индуктор и чистый конденсатор её не потребляют.

В чистом резистивном контуре ток находится в фазе с приложенным напряжением, тогда как в чистом индуктивном и ёмкостном контуре ток смещён на 90 градусов: если индуктивная нагрузка подключена в сеть, он теряет напряжение на 90 градусов. При подключении ёмкостной нагрузки происходит смещение тока на 90 градусов в обратную сторону.

В первом случае создаётся активная мощность, а во втором — реактивная.

Силовой треугольник

Полная мощность — это векторная сумма активной и реактивной мощности. Элементы полной мощности:

• Активная, P.
• Реактивная, Q.
• Полная, S.

Реактивная мощность не работает, она представлена как мнимая ось векторной диаграммы. Активная мощность работает и является реальной стороной треугольника. Из этого принципа разложения мощностей понятно, в чём измеряется активная мощность. Единицей для всех видов мощности является ватт (W), но это обозначение обычно закрепляется за активной составляющей. Полная мощность условно выражается в ВА .

https://www.youtube.com/watch?v=QBPe-8daSOs

Единица для Q составляющей выражается как var, что соответствует реактивному вольт-амперу. Она не передаёт никакой чистой энергии нагрузке, тем не менее она выполняет важную функцию в электрических сетях. Математическая связь между ними может быть представлена векторами или выражена с использованием комплексных чисел, S = P + j Q (где j — мнимая единица).

Расчёт энергии и мощности

Средняя мощность P в ваттах (W) равна энергии, потребляемой E в джоулях (J), делённой на период t в секундах (секундах): P (W) = E (J) / Δ t (s).

Когда ток и напряжение находятся на 180 градусов по фазе, PF отрицательный, нагрузка подаёт электроэнергию в источник (примером может служить дом с солнечными батареями на крыше, которые подают питание в энергосистему). Пример:

• P составляет 700 Вт, а фазовый угол составляет 45, 6;
• PF равен cos (45, 6) = 0, 700. Тогда S = 700 Вт / cos (45, 6) = 1000 В⋅А.

Отношение активной к полной мощности называется коэффициентом мощности (PF). Для двух систем, передающих такое же количество активной нагрузки, система с более низким PF будет иметь большие оборотные токи из-за электроэнергии, которая возвращается обратно. Эти большие токи создают большие потери и снижают общую эффективность передачи. Схема с более низким PF будет иметь большую полную нагрузку и более высокие потери для одинакового количества активной нагрузки. PF = 1, 0, когда есть фазный ток. Он равен нулю, когда ток приводит или отстаёт от напряжения на 90 градусов.

Например, PF =0,68 и означает, что только 68 процентов от общего объёма поставленного тока фактически выполняют работу, остальные 32 процента являются реактивными. Производители коммунальных услуг не берут с потребителей плату за её реактивные потери. Однако если в источнике нагрузки клиента есть неэффективность, которая приводит к тому, что PF падает ниже определённого уровня, коммунальные услуги могут взимать плату с клиентов, чтобы покрыть увеличение использования топлива на электростанциях и ухудшение линейных показателей сети.

Характеристики полной S

Формула полной мощности зависит от активной и реактивной мощности и представлена как энергетический треугольник (Теорема Пифагора). S = (Q 2 + P 2) 1 / 2, где:

• S = полная (измерение в киловольт-ампер, кВА);
• Q = реактивная (реактивность на киловольтах, kVAR);
• P = активная (киловатт, кВт).

Она измеряется во вольт-амперах (В⋅А) и зависит от напряжения, умноженного на весь поступающий ток. Это векторная сумма P и Q составляющих, которая подсказывает, как найти полную мощность. Однофазная сеть: V (V) = I (A) x R (Ω).

P (W) = V (V) x I (A) = V 2 (V) / R (Ω) = I 2 (A) x R (Ω).

Трёхфазная сеть:

Напряжение V в вольтах (V) эквивалентно току I в амперах (A), умноженному на импеданс Z в омах (Ω):

V (V) = I (A) x Z (Ω) = (| I | x | Z |) ∠ ( θ I + θ Z ).

S (VA) = V (V) x I (A) = (| V | x | I |) ∠ ( θ V — θ I ).

Активная P

Это мощность, которая используется для работы, её активная часть, измеряемая во Вт и является силой, потребляемой электрическим сопротивлением системы. P (W) = V (V) x I (A) x cos φ

Реактивная Q

Она не используется для работы в сети. Q измеряется в вольт-амперах (VAR). Увеличение этих показателей приводит к уменьшению коэффициента мощности (PF). Q (VAR) = V (V) x I (A) x sin φ.

Коэффициент эффективности сетей

PF определяется размерами P и S, его вычисляют по теореме Пифагора. Рассматривается косинус угла между напряжением и током (несинусоидальный угол), фазовая диаграмма напряжения или тока от энергетического треугольника. Коэффициент PF равен абсолютному значению косинуса комплексного энергетического фазового угла (φ): PF = | cosφ | Эффективность энергосистемы зависит от коэффициента PF и для повышения эффективности использования в энергосистеме необходимо его увеличивать.

Ёмкостные и индуктивные нагрузки

Сохранённая энергия в электрическом и магнитном полях в условиях нагрузки, например, от двигателя или конденсатора, вызывает смещение между напряжением и током. Поскольку ток протекает через конденсатор, накапливание заряда вызывает возникновение противоположного напряжения на нём. Это напряжение увеличивается до некоторого максимума, продиктованного структурой конденсатора. В сети с переменным током на конденсаторе постоянно меняется напряжение. Конденсаторы называются источником реактивных потерь и, таким образом, вызывают ведущий PF.

Индукционные машины являются одними из наиболее распространённых типов нагрузок в электроэнергетической системе. Эти машины используют индукторы или большие катушки проволоки для хранения энергии в виде магнитного поля. Когда напряжение сначала проходит через катушку, индуктор сильно сопротивляется этому изменению тока и магнитного поля, что создает задержку времени с максимальным значением. Это приводит к тому, что ток отстаёт от напряжения по фазе.

Индукторы поглощают Q и, следовательно, вызывают запаздывающий PF. Индукционные генераторы могут подавать или поглощать Q и обеспечивать меру управления системными операторами по потоку Q и по напряжению. Поскольку эти устройства оказывают противоположное воздействие на фазовый угол между напряжением и током, их можно использовать для отмены эффектов друг друга. Обычно это принимает форму конденсаторных банков, используемых для противодействия запаздывающим PF, вызванным асинхронными двигателями.

Погашения реактивного влияния в электросетях

Активная реактивная и полная мощность определяет PF главный фактор для оценки эффективности использования электроэнергии в сети энергосистемы. Если PF высокий, то, можно сказать, что более эффективно электроэнергия используется в энергосистеме. Поскольку PF плох или уменьшается, эффективность использования электроэнергии в энергосистеме снижается. Низкий PF или снижение его обусловлены различными причинами. Для повышения PF существуют специальные способы коррекции.

Использование конденсаторов является наилучшим и эффективным способом повышения эффективности сети. Метод, известный как реактивная компенсация, используется для уменьшения кажущегося потока мощности на нагрузку за счёт уменьшения реактивных потерь. Например, для компенсации индуктивной нагрузки шунтирующий конденсатор устанавливается вблизи самой нагрузки. Это позволяет потреблять конденсатором всю Q и не передавать их по линиям передачи.

Эта практика экономит энергию, потому что она уменьшает количество энергии, которое требуется, для выполнения того же объёма работы. Кроме того, она позволяет использовать более эффективные конструкции линий электропередачи с использованием меньших проводников или меньшего количества проводников с разъёмами и оптимизировать конструкцию трансмиссионных вышек.

Чтобы поддерживать напряжение в оптимальном диапазоне и предотвращать явления нестабильности, в оптимальных местах по всей сети энергосистемы устанавливаются различные устройства для фазовой регулировки, а также используются различные методы реактивного управления.

Предложенная система делит традиционный метод на управление напряжением и Q:

• управление напряжением для регулировки напряжения вторичной шины подстанций;
• регулирование Q для регулирования напряжения первичной шины.

В этой системе на подстанциях установлены два типа устройств для взаимодействия контроля напряжения и контроля Q.

Управление напряжением и реактивной мощностью

Это два аспекта одного воздействия, которые поддерживают надёжность и облегчают коммерческие транзакции в сетях передачи. На силовой системе переменного тока (AC) напряжение контролируется путём управления производством и поглощением Q. Существует три причины, по которым необходим такой вид управления:

1. Оборудование энергосистемы предназначено для работы в диапазоне напряжений, обычно в пределах ± 5% от номинального напряжения. При низком напряжении оборудование работает плохо, лампочки обеспечивают меньшую освещённость, асинхронные двигатели могут перегреваться и быть повреждёнными, а некоторые электронные устройства не будут работать вообще. Высокие напряжения могут повредить оборудование и сократить срок его службы.
2. Q потребляет ресурсы передачи и генерации. Чтобы максимизировать реальную мощность, которая может быть передана через перегруженный интерфейс передачи, потоки Q должны быть минимизированы. Аналогичным образом производство Q может ограничить реальную мощность генератора.
3. Движущая реактивность в передающей сети несёт реальные потери мощности. Для восполнения этих потерь должны компенсироваться мощность и энергия.

Система передачи является нелинейным потребителем Q в зависимости от загрузки системы. При очень низкой нагрузке система генерирует Q, которая должна поглощаться, а при большой нагрузке система потребляет большое количество Q, которую необходимо заменить. Требования к Q системы также зависят от конфигурации генерации и передачи. Следовательно, системные реактивные требования меняются во времени по мере изменения уровней нагрузки и моделей нагрузки и генерации.

Работа системы имеет три цели управления Q и напряжениями:

1. Она должна поддерживать достаточное напряжение во всей системе передачи и распределения как для текущих, так и для непредвиденных условий.
2. Обеспечить минимизацию перегрузки реальных потоков энергии.
3. Стремиться минимизировать реальные потери мощности.

Объёмная энергетическая система состоит из множества единиц оборудования, любая из которых может быть неисправна. Таким образом, система предназначена для того, чтобы выдерживать выход из строя отдельного оборудования, продолжая работать в интересах потребителей. Вот почему электрическая система требует реальных резервов мощности для реагирования на непредвиденные обстоятельства и поддержания резервов Q.

Источник: https://220v.guru/fizicheskie-ponyatiya-i-pribory/moschnost/izmerenie-aktivnoy-reaktivnoy-i-polnoy-moschnosti.html

Активная и реактивная мощность. За что платим и работа

Активная и реактивная мощность — потребители электрической энергии на то и потребители, чтобы эту энергию потреблять. Потребителя интересует та энергия, потребление которой идет ему на пользу, эту энергию можно назвать полезной, но в электротехнике ее принято называть активной. Это энергия, которая идет на нагрев помещений, готовку пищи, выработку холода, и превращаемая в механическую энергию (работа электродрелей, перфораторов, электронасосов и пр.).

Кроме активной электроэнергии существует еще и реактивная. Это та часть полной энергии, которая не расходуется на полезную работу. Как понятно из вышесказанного, полная мощность – это активная и реактивная мощность в целом.

В понятиях активная и реактивная мощность сталкиваются противоречивые интересы потребителей электрической энергии и ее поставщиков. Потребителю выгодно платить только за потребленную им полезную электроэнергию, поставщику выгодно получать оплату за сумму активной и реактивной электроэнергии. Можно ли совместить эти кажущиеся противоречивыми требования? Да, если свести количество реактивной электроэнергии к нулю. Рассмотрим, возможно ли подобное, и насколько можно приблизиться к идеалу.

Активная мощность

Существуют потребители электроэнергии, у которых полная и активная мощности совпадают. Это потребители, у которых нагрузка представлена активными сопротивлениями (резисторами). Среди бытовых электроприборов примерами подобной нагрузки являются лампы накаливания, электроплиты, жарочные шкафы и духовки, обогреватели, утюги, паяльники и пр.

Указанная у этих приборов в паспорте, одновременно является активная и реактивная мощность . Это тот случай, когда мощность нагрузки можно определить по известной из школьного курса физики формуле, перемножив ток нагрузки на напряжение в сети. Ток измеряется в амперах (А), напряжение в вольтах (В), мощность в ваттах (Вт). Конфорка электрической плиты в сети с напряжением 220 В при токе в 4,5 А потребляет мощность 4,5 х 220 = 990 (Вт).

Реактивная мощность

Иногда, проходя по улице, можно увидеть, что стекла балконов покрыты изнутри блестящей тонкой пленкой. Эта пленка изъята из бракованных электрических конденсаторов, устанавливаемых с определенными целями на питающих мощных потребителей электрической энергии распределительных подстанциях. Конденсатор – типичный потребитель реактивной мощности.

В отличие от потребителей активной мощности, где главным элементом конструкции является некий проводящий электричество материал (вольфрамовый проводник в лампах накаливания, нихромовая спираль в электроплитке и т.п.). В конденсаторе главный элемент – не проводящий электрический ток диэлектрик (тонкая полимерная пленка или пропитанная маслом бумага).

Реактивная емкостная мощность

Красивые блестящие пленки, что вы видели на балконе – это обкладки конденсатора из токопроводящего тонкого материала. Конденсатор замечателен тем, что он может накапливать электрическую энергию, а затем отдавать ее – своеобразный такой аккумулятор. Если включить конденсатор в сеть постоянного тока, он зарядится кратковременным импульсом тока, а затем ток через него протекать не будет.

Вернуть конденсатор в исходное состояние можно, отключив его от источника напряжения и подключив к его обкладкам нагрузку. Некоторое время через нагрузку будет течь электрический ток, и идеальный конденсатор отдает в нагрузку ровно столько электрической энергии, сколько он получил при зарядке.

Подключенная к выводам конденсатора лампочка может на короткое время вспыхнуть, электрический резистор нагреется, а неосторожного человека может «тряхнуть» или даже убить при достаточном напряжении на выводах и запасенном количестве электричества.

Интересная картина получается при подключении конденсатора к источнику переменного электрического напряжения. Поскольку у источника переменного напряжения постоянно меняются полярность и мгновенное значение напряжения (в домашней электросети по закону, близкому к синусоидальному). Конденсатор будет непрерывно заряжаться и разряжаться, через него будет непрерывно протекать переменный ток. Но этот ток не будет совпадать по фазе с напряжением источника переменного напряжения, а будет опережать его на 90°, т.е. на четверть периода.

Это приведет к тому, что суммарно половину периода переменного напряжения конденсатор потребляет энергию из сети, а половину периода отдает, при этом суммарная потребляемая активная электрическая мощность равна нулю. Но, поскольку через конденсатор течет значительный ток, который может быть измерен амперметром, принято говорить, что конденсатор – потребитель реактивной электрической мощности

Вычисляется реактивная мощность как произведение тока на напряжение, но единица измерения уже не ватт, а вольт-ампер реактивный (ВАр). Так, через подключенный к сети 220 В частотой 50 Гц электрический конденсатор емкостью 4 мкФ течет ток порядка 0,3 А. Это означает, что конденсатор потребляет 0,3 х 220 = 66 (ВАр) реактивной мощности – сравнимо с мощностью средней лампы накаливания, но конденсатор, в отличие от лампы, при этом не светится и не нагревается.

Реактивная индуктивная мощность

Если в конденсаторе ток опережает напряжение, то существуют ли потребители, где ток отстает от напряжения? Да, и такие потребители, в отличие от емкостных потребителей, называются индуктивными, оставаясь при этом потребителями реактивной энергии. Типичная индуктивная электрическая нагрузка – катушка с определенным количеством витков хорошо проводящего провода, намотанного на замкнутый сердечник из специального магнитного материала.

На практике хорошим приближением чисто индуктивной нагрузки является работающий без нагрузки трансформатор (или стабилизатор напряжения с автотрансформатором). Хорошо сконструированный трансформатор на холостом ходу потребляет очень мало активной мощности, потребляя мощность в основном реактивную.

Реальные потребители электрической энергии и полная электрическая мощность

Из рассмотрения особенностей емкостной и индуктивной нагрузки возникает интересный вопрос – что произойдет, если емкостную и индуктивную нагрузку включить одновременно и параллельно. Ввиду их противоположной реакции на приложенное напряжение, эти две реакции начнут компенсировать друг друга.

Суммарная нагрузка окажется только емкостной или индуктивной, и в некотором идеальном случае удастся добиться полной компенсации. Выглядеть это будет парадоксально – подключенные амперметры зафиксируют значительные (и равные!) токи через конденсатор и катушку индуктивности, и полное отсутствие тока в объединяющих их общей цепи.

Описанная картина несколько нарушается лишь тем, что не существует идеальных конденсаторов и катушек индуктивности, но подобная идеализация помогает понять суть происходящих процессов.

Вернемся к реальным потребителям электрической энергии. В быту мы пользуемся в основном потребителями чисто активной мощности (примеры приведены выше), и смешанной активно-индуктивной. Это электродрели, перфораторы, электродвигатели холодильников, стиральных машин и прочей бытовой техники.

Также к ним относятся электрические трансформаторы источников питания бытовой радиоэлектронной аппаратуры и стабилизаторов напряжения. В случае подобной смешанной нагрузки, помимо активной (полезной) мощности, нагрузка потребляет еще и реактивную мощность, в итоге полная мощность отказывается больше активной мощности.

Полная мощность измеряется в вольт-амперах (ВА), и всегда представляет собой произведение тока в нагрузке на напряжение на нагрузке.

Таинственный «косинус фи»

Отношение активной мощности к полной называется в электротехнике «косинусом фи». Обозначается cos φ. Это отношение называется также и коэффициентом мощности. Нетрудно видеть, что для случая чисто активной нагрузки, где полная мощность совпадает с активной, cos φ = 1. Для случаев чисто емкостной или индуктивной нагрузок, где нулю равна активная мощность, cos φ = 0.

В случае смешанной нагрузки значение коэффициента мощности заключается в пределах от 0 до 1. Для бытовой техники обычно в диапазоне 0,5-0,9. В среднем можно считать его равным 0,7, более точное значение указывается в паспорте электроприбора.

За что платим?

И, наконец, самый интересный вопрос – за какой вид энергии платит потребитель. Исходя из того, что реактивная составляющая суммарной энергии не приносит потребителю никакой пользы, при этом долю периода реактивная энергия потребляется, а долю отдается, платить за реактивную мощность незачем.

Но бес, как известно, кроется в деталях.

Поскольку смешанная нагрузка увеличивает ток в сети, возникают проблемы на электростанциях, где электроэнергия вырабатывается синхронными генераторами, а именно: индуктивная нагрузка «развозбуждает» генератор, и приведение его в прежнее состояние обходится в затраты уже реальной активной мощности на его «довозбуждение».

Таким образом, заставить потребителя платить за потребляемую реактивную индуктивную мощность вполне справедливо. Это побуждает потребителя компенсировать реактивную составляющую своей нагрузки, а, поскольку эта составляющая в основном индуктивная, компенсация заключается в подключении конденсаторов наперед рассчитанной емкости.

Потребитель находит возможность платить меньше

Если потребителем оплачивается отдельно потребляемая активная и реактивная мощность. Он готов идти на дополнительные затраты и устанавливать на своем предприятии батареи конденсаторов, включаемые строго по графику в зависимости от средней статистики потребления электроэнергии по часам суток.

Существует также возможность установки на предприятии специальных устройств (компенсаторов реактивной мощности), подключающих конденсаторы автоматически в зависимости от величины и характера потребляемой в данный момент мощности. Эти компенсаторы позволяют поднять значение коэффициента мощности с 0,6 до 0,97, т.е. практически до единицы.

Принято также, что если соотношение потребленной реактивной энергии и общей не превышает 0,15, то корпоративный потребитель от оплаты за реактивную энергию освобождается

Что же касается индивидуальных потребителей, то, ввиду сравнительно невысокой потребляемой ими мощности, разделять счета на оплату потребляемой электроэнергии на активную и реактивную не принято. Бытовые однофазные счетчики электрической энергии учитывают лишь активную мощность электрической нагрузки, за нее и выставляется счет на оплату. Т.е. в настоящее время даже не существует технической возможности выставить индивидуальному потребителю счет за потребленную реактивную мощность.

Особых стимулов компенсировать индуктивную составляющую нагрузки у потребителя нет, да это и сложно осуществить технически. Постоянно подключенные конденсаторы при отключении индуктивной нагрузки будут бесполезно нагружать подводящую электропроводку. За электросчетчиком (перед счетчиком тоже, но за то потребитель не платит), что вызовет потребление активной мощности с соответствующим увеличением счета на оплату, а автоматические компенсаторы дороги и вряд ли оправдают затраты на их приобретение.

Но, что самое главное, компенсация реактивной энергии у каждого потребителя, от квартиры до огромного предприятия, снизит токи во всех линиях электропитания, от электростанции до квартирного щитка. За счет реактивной составляющей полного тока, что уменьшит потери энергии в линиях и повысит коэффициент полезного действия электросистем.

Похожие темы:

Источник: https://electrosam.ru/glavnaja/jelektrotehnika/aktivnaia-i-reaktivnaia-moshchnost/